\n",
"\n",
"In order to setup your own experiments, you need to download remote files to your linux disk image in the collaboratory environment. As data for your user account is NOT reset when you close or reload the HBP, you have to be very careful how you organize & structure your data. In order to help you with that we create a unique working directory for each molecular use case you run.\n",
"\n",
"Please be also aware that we switch current working directories in this use case. That means that you have to restart and clear all output in order to go back to your starting directory. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "q60O_8CFyazK"
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {
"id": "i-HbQ7WTuwRp"
},
"source": [
"# Analyse the results of a Brownian dynamics simulation for calculating protein-protein association rate constants\n",
"\n",
"**Aim:** This use case shows how to compute a bimolecular association rate constant from Brownian dynamics simulations of the diffusional association of two proteins.\n",
"\n",
"**Version:** 1.0 (March 2019)\n",
"\n",
"**Contributors:** Neil Bruce, Lukas Adam, Stefan Richter, Rebecca Wade (HITS, Heidelberg, Germany)\n",
"\n",
"**Contact:** [mcmsoft@h-its.org](mailto:mcmsoft@h-its.org)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "rr5zxC7wRteo"
},
"source": [
"Please have a look at the live paper [Bruce et al 2019](https://live-papers.brainsimulation.eu/#2019-bruce-et-al) about \"Regulation of adenylyl cyclase 5 in striatal neurons\". There you find examples of electrostatic potentials calculated and displayed (see the resources section).\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "70smbDTLuwRq"
},
"source": [
"## Setting up your environment"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "To2aXmc4uwRq"
},
"source": [
"### Check that all required python packages are installed and working"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "1qdVeRwRuwRr",
"outputId": "41923c3c-d133-4aca-d249-1029e58581fe"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Requirement already satisfied: wget in ./.local/lib/python3.8/site-packages (3.2)\n",
"Requirement already satisfied: python-magic in ./.local/lib/python3.8/site-packages (0.4.27)\n"
]
}
],
"source": [
"# Check that required packages are installed\n",
"\n",
"! pip install wget python-magic"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"id": "gSUaxAZ9uwRt"
},
"outputs": [],
"source": [
"# Import python packages used in this notebook\n",
"import os, wget, warnings, subprocess, datetime\n",
"import os.path\n",
"import pandas as pd\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from pylab import rcParams"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "c6xzCYsDuwRt"
},
"source": [
"### Install SDA software on the notebook server"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "8UPjldQjuwRu",
"outputId": "af80c575-8173-46cb-bcd4-34cac97f480d"
},
"outputs": [],
"source": [
"try:\n",
" JUPYTER_ROOT_DIRECTORY\n",
"except NameError: \n",
" JUPYTER_ROOT_DIRECTORY = os.getcwd()\n",
"# Create a local directory\n",
"try:\n",
" homeDir = JUPYTER_ROOT_DIRECTORY+\"/content\"\n",
"except:\n",
" print(\"Error in environment\")\n",
"\n",
"else:\n",
" workDir = os.path.join(homeDir, 'work')\n",
" if not os.path.isdir(workDir):\n",
" try:\n",
" os.makedirs(workDir)\n",
" except:\n",
" print(\"unable to make working directory: \".workdir)\n",
" \n",
" # Make a new directory to run the use case in. \n",
" # If directory already exists, add a number to make a unique name\n",
" baseDir = 'epCalc'\n",
" dirIter = 0\n",
" useCaseDir = os.path.join(workDir, baseDir)\n",
" pdbdir=os.path.join(useCaseDir,'workshop2022/DATA/PDB')\n",
" \n",
" if os.path.exists(useCaseDir):\n",
" while os.path.exists(useCaseDir):\n",
" dirIter += 1\n",
" useCaseDir = os.path.join(workDir, baseDir + '.' + str(dirIter)) \n",
" \n",
" try:\n",
" os.makedirs(useCaseDir)\n",
" os.chdir(useCaseDir)\n",
" except:\n",
" print(\"Failed to make use case working directory\")\n",
" else:\n",
" print(\"Working directory for current use case: %s\" % useCaseDir)\n",
"#!wget -c https://github.com/cnr-ibf-pa/hbp-bsp-issues/files/4148695/sda_flex-7.2.3-minimal.zip\n",
"#!unzip -o sda_flex-7.2.3-minimal.zip > sdazip.log 2>&1\n",
"#!cd minimal-sda_flex-7.2.3/src && make clean && make > sdamake.log 2>&1"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "8UPjldQjuwRu",
"outputId": "af80c575-8173-46cb-bcd4-34cac97f480d"
},
"outputs": [],
"source": [
"%%bash --out sda_flex\n",
"which sda_flex"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "8UPjldQjuwRu",
"outputId": "af80c575-8173-46cb-bcd4-34cac97f480d"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/srv/main-spack-instance-2302/spack/var/spack/environments/ebrains-23-02/.spack-env/view/bin/sda_flex\n",
"\n",
"/srv/main-spack-instance-2302/spack/var/spack/environments/ebrains-23-02/.spack-env/view/bin/../\n"
]
}
],
"source": [
"os.environ['SDAEXE'] = sda_flex\n",
"os.environ['SDAHOME'] = os.path.dirname(os.environ['SDAEXE'])+\"/../\"\n",
"print(os.environ['SDAEXE'])\n",
"#!ldd /srv/main-spack-instance-2302/spack/var/spack/environments/ebrains-23-02/.spack-env/view/bin/sda_flex\n",
"#!ls /srv/main-spack-instance-2302/spack/var/spack/environments/ebrains-23-02/.spack-env/view/bin/../auxi\n",
"print(os.environ['SDAHOME'])"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "-gE7hkKBuwRv"
},
"source": [
"### Check that SDA is available"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "zQ1DbkxvuwRv",
"outputId": "a502581a-b8c9-417e-bf5b-46f4d3c57712"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"SDA is installed in /srv/main-spack-instance-2302/spack/var/spack/environments/ebrains-23-02/.spack-env/view/bin/../\n",
"Bootstrap file found: /srv/main-spack-instance-2302/spack/var/spack/environments/ebrains-23-02/.spack-env/view/bin/../auxi/Bootstrap_multiCPU.py\n"
]
}
],
"source": [
"# Check that SDA is environment variable is set\n",
"try:\n",
" sdaDir = os.environ['SDAHOME']\n",
"except:\n",
" print(\"Unable to find SDA. There is a problem\")\n",
"else:\n",
" print(\"SDA is installed in %s\" % sdaDir)\n",
" \n",
"# Check that bootstrap script used in this use case is available\n",
"bootScr = os.path.join(sdaDir, 'auxi', 'Bootstrap_multiCPU.py')\n",
"if os.path.isfile(bootScr):\n",
" print (\"Bootstrap file found: %s\" % bootScr)\n",
"else:\n",
" print(\"Bootstrap file is not found. There is an error in the SDA installation.\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "nik1d2B6uwRw"
},
"source": [
"### Set up local directory and download required files"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "nVrY0_unuwRw",
"outputId": "7ce008a1-f679-4d13-e10b-74f1b6118959"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Working directory for current use case: /opt/app-root/src/content/work/sdaAnalysis\n"
]
}
],
"source": [
"try:\n",
" JUPYTER_ROOT_DIRECTORY\n",
"except NameError: \n",
" JUPYTER_ROOT_DIRECTORY = os.getcwd()\n",
"# Create a local directory\n",
"try:\n",
" homeDir = JUPYTER_ROOT_DIRECTORY+\"/content\"\n",
"except:\n",
" print(\"Error in environment\")\n",
"\n",
"else:\n",
" workDir = os.path.join(homeDir, 'work')\n",
" if not os.path.isdir(workDir):\n",
" try:\n",
" os.makedirs(workDir)\n",
" except:\n",
" print(\"unable to make working directory: \".workdir)\n",
" \n",
" # Make a new directory to run the use case in. \n",
" # If directory already exists, add a number to make a unique name\n",
" baseDir = 'sdaAnalysis'\n",
" dirIter = 0\n",
" useCaseDir = os.path.join(workDir, baseDir)\n",
" pdbdir=os.path.join(useCaseDir,'workshop2022/DATA/PDB')\n",
" \n",
" if os.path.exists(useCaseDir):\n",
" while os.path.exists(useCaseDir):\n",
" dirIter += 1\n",
" useCaseDir = os.path.join(workDir, baseDir + '.' + str(dirIter)) \n",
" \n",
" try:\n",
" os.makedirs(useCaseDir)\n",
" os.chdir(useCaseDir)\n",
" except:\n",
" print(\"Failed to make use case working directory\")\n",
" else:\n",
" print(\"Working directory for current use case: %s\" % useCaseDir)\n"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "m-QUqcrBuwRx",
"outputId": "dacf3735-0f86-4e0a-fd44-62b7ae01bad3"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Downloading SDA bootstrap output file from CSCS storage area\n",
"Sucessfully downloaded the bootstrap output file from CSCS storage\n"
]
}
],
"source": [
"# Download SDA bootstrap output file from CSCS storage for analysis\n",
"try:\n",
" print(\"Downloading SDA bootstrap output file from CSCS storage area\")\n",
" fileUrl= 'https://object.cscs.ch/v1/AUTH_c0a333ecf7c045809321ce9d9ecdfdea/SGA2_molecular_signalling_cascades/data/Predicted_association_rate_constants_of_G_proteins_to_AC5_complexes/bootstrap_logfiles/holo_kf3_AC5-Golf_Gi/snap_0/rep_1/assoc_bootstrap.log'\n",
" wget.download(fileUrl, useCaseDir)\n",
"except:\n",
" print(\"Error downloading bootstrap output file from CSCS storage\")\n",
"else:\n",
" print(\"Sucessfully downloaded the bootstrap output file from CSCS storage\")\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Pmt1NzCquwRy"
},
"source": [
"**If all of the above cells have completed without error, your python environment and local directories are set up correctly, and you have all the files required for this use case.**"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ZsrekldBuwRz"
},
"source": [
"# Simulation of Diffusional Association - Analysis # "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "3C66MoWouwRz"
},
"source": [
"In this use case, we analyse the results of an [SDA](https://collab.humanbrainproject.eu/#/collab/19/nav/2108?state=software,SDA) simulation of the association of the Golf α-subunit to the enzyme adenylyl cyclase 5 (AC5) [*An upcoming BSP use case will explain how to set up and run these simulations*]. This use case will explain:\n",
"* The functionality provided by SDA to calculate the biomolecular rate of Gαolf associating to AC5 by analysing the contact formation between the two protein species during a set of 50 000 completed Brownian dynamics simulation trajectories.\n",
"* The use of a bootstrapping procedure to estimate the error in the predicted rates.\n",
"* The use of matplotlib to plot the dependence of association rates on how we define the end point of association based on contact formation.\n",
"\n",
"** Recap: How is protein diffusion modeled in Brownian dynamics simulations? **\n",
"\n",
"As the interaction of large biomolecules in solution is a highly complex problem with many degrees of freedom, the diffusional motion of proteins in Brownian dynamics simulations is often modelled by assuming the proteins to be rigid bodies. Furthermore, their interactions with surrounding water molecules are modeled implicitly (using random forces that mimic the collisions between solutes and water molecules). These assumptions not only speed up the calculation of the systematic forces by allowing the use of precomputed interaction grids, but also allow for larger simulation time steps, as faster vibrational motions are removed. At each simulation step, the position $r$ of solute $i$ within a system of $N$ solutes is propagated using the Ermak-McCammon equation:\n",
"\n",
"$$ \\Delta r_{i} = \\Delta t\\sum_{j=1}^{N}\\left ( \\frac{\\partial \\widehat{D}_{ij}}{\\partial r_{j}} + \\frac{\\widehat{D}_{ij}}{k_{B}T} \\cdot F_{i} \\right ) + R_{i} $$\n",
"\n",
"where $k_{B}$ and $T$ are the Boltzmann constant and simulation temperature, respectively, and $F_{i}$ is the force acting on solute $i$ due to its interactions with all other solutes. $\\mathbf{\\widehat{D}}$ is the diffusion tensor for the current configuration of the system, and $R_{i}$ is a random displacement vector obtained from the factorisation of $\\mathbf{\\widehat{D}}$. The dependence of the diffusion of one solute on the diffusion of all other solutes is due to hydrodynamic interactions, where solutes are able to feel the flow fields in solution created by the other solutes. \n",
"\n",
"Modelling hydrodynamic interactions is extremely computationally expensive, due to the need to factorise $\\mathbf{\\widehat{D}}$ at every time step. In dilute conditions, as we use rigid solutes, we can assume these interactions are negligible, simplifying the equation and removing the need for matrix factorisation:\n",
"\n",
"$$ \\Delta r_{i} = \\frac{\\Delta t}{k_{B}T} D_{i}^{T} \\cdot F_{i} + R_{i} $$\n",
"\n",
"where $ D_{i}^{T}$ is the infinite dilution translational diffusion coefficient of solute $i$, and $R_{i}$ is a random vector sampled from a Gaussian distribution with mean zero and a variance of $\\left \\langle R_{i}^{2} \\right \\rangle = 6D_{i}^{T} \\Delta t$. A similar equation is used to propagate the rotational motion of the solutes based on the torques acting on them.\n",
"\n",
"For information on the calculation of the contributions to the force $F_{i}$, see [Martinez et al (2015), Journal of Computational Chemistry, 36, 1631–1645](https://mcm.h-its.org/sda7/doc/doc_sda7/jcc23971.pdf).\n",
"\n",
"\n",
"** Prediction of bimolecular association rate constant **\n",
"\n",
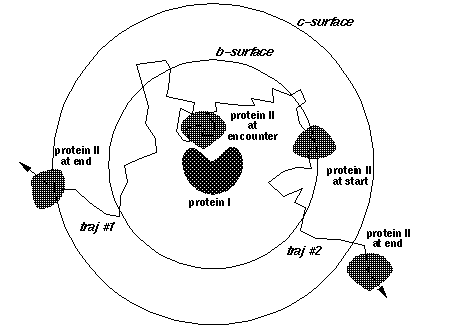
"SDA calculates bimolecular association rate constants using the [Northrup, Allison and McCammon](https://doi.org/10.1063/1.446900) method. Here we run many thousands of Brownian dynamics trajectories, each beginning with the two solutes (molecules, in this case proteins) at a separation $b$ (shown by the b-surface in the figure below). In each trajectory, we then simulate the diffusion of one solute relative to another, until the solutes are separated by a larger distance $c$ (shown by the c-surface in the figure below).\n",
"\n",
"\n",
"\n",
"During each trajectory, we monitor the formation of polar contacts present in the native state of the complex formed by the two solutes. If we define a set of reaction criteria that says a reactive encounter occurs when $N$ native contacts are within a certain distance, we can calculate the fraction $\\beta$ of our trajectories in which these criteria are met, and estimate the bimolecular association rate constant $k_{on}$ from\n",
"\n",
"$$k_{on} = \\frac{k_b\\beta}{1-(1-\\beta)\\frac{k_b}{k_c}}$$\n",
"\n",
"where $k_b$ and $k_c$ are the rates at which the solutes diffuse to separations $b$ and $c$, respectively. If we assume the interactions between the solutes do not depend on their relative orientations at these large distances, these rates can be calculated analytically.\n",
"\n",
"\n",
"** The assoc_bootstrap.log file downloaded from CSCS storage **\n",
"\n",
"In the set up cells run at the top of this notebook, we downloaded a file called *assoc_bootstrap.log*. This file gives a concise representation of the results of 50 000 Brownian dynamics simulation trajectories. The header to the file gives some information about the simulations that have been run.\n",
"\n",
"\n",
"nb_contact | nb_wind | first_win | width_win | b_rate | c_rate | nrun |\n",
"------------|----------|-----------|-----------|--------------|--------------|-------|\n",
" 4 | 35 | 3.00 | 0.50 | 0.231552E+11 | 0.694655E+11 | 50000 |\n",
"\n",
"In each trajectory, we monitor the formation of up to *nb_contact* native contacts over *nb_wind* distance windows of *width_win* Å, starting from a distance of *first_win* Å. The *b_rate* and *c_rate*, correspond to $k_b$ and $k_c$ in the equation above. In total, *nrun* trajectories were run. The rest of the file is separated into sections corresponding to each number of contacts that we monitor. Each line represents a single trajectory, and contains a number showing the closest window at which that number of contacts was obtained during the trajectory.\n",
"\n",
"\n",
"** What is bootstrapping? **\n",
"\n",
"Bootstrapping is defined as any test or metric that relies on random resampling with replacement. It allows us to assign measures of accuracy (e.g. confidence intervals, standard deviations or standard errors) to sample estimates. By randomly resampling the data, one can approximate the underlying statistical distribution. \n",
"\n",
"The SDA script *Bootstrap_multiCPU.py* analyses the *assoc_bootstrap.log* file to predict rate constants for various encounter definitions. It then performs bootstrapping to estimate the standard deviation in the prediction across a set of resampled trajectories.\n",
"\n",
"** Outline of the analysis below**\n",
"\n",
"During the 50 000 trajectories described in the log file, we monitor the formation of up to 4 native contacts. In the cells below, we perform bootstrapping by randomly resampling 200 sets of 50 000 trajectories. From there, we will extract the values and convert them to a pandas dataframe, which will then be plotted with matplotlib, and we save summary data to a set of output files. "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "qH17jEWduwR0"
},
"source": [
"### Run bootstrapping analysis on SDA bootstrap output file"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "n-nMjeX5uwR0",
"outputId": "79143221-f55f-4a78-ae9e-cf4a1d9463e8"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/opt/app-root/src/content/work/sdaAnalysis/assoc_bootstrap.log /srv/main-spack-instance-2302/spack/var/spack/environments/ebrains-23-02/.spack-env/view/bin/../auxi/Bootstrap_multiCPU.py\n"
]
}
],
"source": [
"warnings.filterwarnings('ignore')\n",
"%matplotlib inline\n",
"\n",
"# Move to the working directory for this use case\n",
"os.chdir(useCaseDir)\n",
" \n",
"assoc_bootstrap_log = os.path.join(useCaseDir, 'assoc_bootstrap.log')\n",
"print(assoc_bootstrap_log, bootScr)"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "H-vfTLVUuwR0",
"outputId": "0f578a68-fad0-4b7d-d74e-e55fee358056",
"tags": []
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Please Note, This calculation takes some time\n"
]
}
],
"source": [
"# Run the bootstrap analysis script on the SDA output file\n",
"\n",
"# Output from the scripts is saved into a list of pandas data frames for \n",
"# different number of contacts\n",
"\n",
"# Create a dataframe for current contact number\n",
"def kin2pandas(contact):\n",
" return pd.DataFrame([list(filter(None, i.split(' '))) for i in list(filter(None, contact))])\n",
"\n",
"# Create list of contacts\n",
"def get_contacts(kin):\n",
" indices = [0] + [i for i, x in enumerate(kin) if x == \"\"] + [len(kin)]\n",
" contacts = []\n",
" for i in range(len(indices)-1):\n",
" contacts.append(kin[indices[i]:indices[i+1]])\n",
" contacts = [kin2pandas(contact) for contact in contacts]\n",
" return contacts\n",
"\n",
"# Run Bootstrap analysis script on SDA output file\n",
"def extract_kinetics(sda_bootstrap, assoc_bootstrap_log):\n",
" cmd = ['python', sda_bootstrap, '-i', assoc_bootstrap_log]\n",
" p = subprocess.Popen(cmd, stdout=subprocess.PIPE)\n",
" p = list(p.communicate())[0].decode(\"utf-8\").split('\\n')\n",
" p = [i.strip() for i in p]\n",
" p = p[p.index('# distance average std.deviation')+1:]\n",
" kin = get_contacts(p)\n",
" return kin\n",
" \n",
"print(\"Please Note, This calculation takes some time\")\n",
"kin = extract_kinetics(bootScr, assoc_bootstrap_log)"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 206
},
"id": "hQN55G6GuwR1",
"outputId": "cc1cd385-6769-4701-de92-d769fba59f3d"
},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
0
\n",
"
1
\n",
"
2
\n",
"
\n",
" \n",
" \n",
"
\n",
"
0
\n",
"
3.000
\n",
"
0.00000e+00
\n",
"
0.00000e+00
\n",
"
\n",
"
\n",
"
1
\n",
"
3.500
\n",
"
3.71801e+06
\n",
"
1.64415e+06
\n",
"
\n",
"
\n",
"
2
\n",
"
4.000
\n",
"
6.69215e+06
\n",
"
2.19354e+06
\n",
"
\n",
"
\n",
"
3
\n",
"
4.500
\n",
"
1.78431e+07
\n",
"
3.91456e+06
\n",
"
\n",
"
\n",
"
4
\n",
"
5.000
\n",
"
4.01349e+07
\n",
"
5.54065e+06
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" 0 1 2\n",
"0 3.000 0.00000e+00 0.00000e+00\n",
"1 3.500 3.71801e+06 1.64415e+06\n",
"2 4.000 6.69215e+06 2.19354e+06\n",
"3 4.500 1.78431e+07 3.91456e+06\n",
"4 5.000 4.01349e+07 5.54065e+06"
]
},
"execution_count": 57,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Loading dataframe for one contact to check rates have been calculated\n",
"kin[0].head()"
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"id": "CHDjE3aXuwR1",
"tags": []
},
"outputs": [],
"source": [
"def write_summary(kin):\n",
" contactsFiles = []\n",
" for i in range(len(kin) - 1):\n",
" nContacts = i+1\n",
" file = 'contacts_' + str(nContacts) + '.dat'\n",
" fr = kin[i]\n",
" fr.columns = ['#Dist', 'Rate M-1s-1', 'std dev']\n",
" fr.to_csv(file, index=False, sep='\\t')\n",
" contactsFiles.append(file)\n",
" return contactsFiles\n",
"\n",
"# Write data for all numbers of contacts to files\n",
"contactsFiles = write_summary(kin)"
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"id": "H-WsUBlBuwR1",
"tags": []
},
"outputs": [],
"source": [
"\n",
"rcParams['figure.figsize'] = 10, 8\n",
"\n",
"def plot_errorbar_kinetics(kinetics, path_to_save_file, filename):\n",
" lines = []\n",
" labels = []\n",
" ax = plt.axes()\n",
" ax.set_yscale(\"log\", nonpositive='clip')\n",
" for index in range(len(kinetics)-1):\n",
" kinetics[index].columns = ['distance', 'average', 'std.deviation']\n",
" kinet = kinetics[index].astype('float32')\n",
" x = kinet.loc[:, 'distance'].tolist()\n",
" y = kinet.loc[:,'average']\n",
" yerr = kinet.loc[:,'std.deviation']\n",
" line = ax.errorbar(x, y, yerr=yerr, fmt='o')\n",
" labels.append('Contacts: ' + str(index+1))\n",
" lines.append(line)\n",
" plt.legend(lines, labels)\n",
" plt.title('SDA Bootstrapping: Contact distance vs. average association rate')\n",
" plt.xlabel('distance (A)')\n",
" plt.ylabel('average association rate (M-1 s-1)')\n",
" plt.savefig(os.path.join(path_to_save_file, filename))\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 513
},
"id": "pvZvYqoeuwR2",
"outputId": "65e585ad-ecec-4c97-a0cc-9467dd47e4cb"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmQAAAHwCAYAAAAIDnN0AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAABk6UlEQVR4nO3de3xU9Z3/8dfHACYihqpFEvCGWJA7GKiaSgW2eMlmq11XdF1tsVtr96cG2qXFVWmK29atXblUd1drS9XdukGKtGnwVkVc0LYJtygoXlAUEhC1BIXEQPj+/jhnYhJmJjOZTM5c3s/HYx6Z+Z7LfObMZPLJ+X7P52vOOUREREQkOEcFHYCIiIhItlNCJiIiIhIwJWQiIiIiAVNCJiIiIhIwJWQiIiIiAVNCJiIiIhIwJWQiATGzzWZ2QdBxpDMzKzez//bvn2JmH5tZTtBxSeYzs/PNbGsC2/+Xmd3enTFJelNCluXM7Atm9oKZNZjZh2a21swm+su+ZmYt/h+5j83sLTNbYmafC7OfC8zMmdl3O3m+C8zscJt97jSzH3TTa2n94xzDul8zszXd8bxd5Zwb6Zx7rieey8wKzOwXZlZvZh+Z2atm9gMz65vgfk/z3/de3RBjQu+Jc+4d59yxzrmWZD6PCIBz7v+cc8NiWTfcZ845d4Nz7o7kRBcf/3d4aNBxZDslZFnMzI4Dfg/8DDgeGAT8APikzWovOueOBfKBvwIagXVmNqrD7r4KfOj/7Eyd/4fzWOALwNfN7NJEXksyZMqZFjM7HngRyAPOdc71A74E9AfOCDA0yRCZ8ruSibrjnyXpIc453bL0BhQBe6Ms/xqwJkz774FlbR4fA3wEXAk0A0VR9nkBsKND21LgX9o8Pg+oBhr8n+e1WVYI/A4v+XsD+IbffpH/3AeBj4FNbV7DNj++t4CrgbOAJqDFX3evv+6vgP8EVgL78RLQEmADsA94FyhvE8tpgAOuB+qAeuA7bZaXA8uACv/51wNj2yx/G/irNusuBR7y193c9jgCE/w4PgIe9ff5rzG+z/8KvAQcFWWdaMf8OeAOYK3//E8BJ/rL3vGPwcf+7Vy8JO9Z4APgfeB/gP5t9ncysBzY469zT6T3JEycpwOr/Tie9rf97w7vR68uvPexvM9f9V/v+8CtbZbnAP8CvOk/1zrgZH/ZcD/OD4GtwBURXteVQE2HttnA7/z7lwBb/P3vBP45xvc+2ut6Arixw/qbgK90Fjtx/q7421wLbPff89tp//k/CpjrH8MP8H4Xjo/wmj6D9x20B/iLf39wh++tdu+73z7U/+w0+O9hRYyf/+OBJXi/438BVoT7LmsT/0f+e3WZ3x7t++Zf22z/DbzvtA/xvuMK2yxzwA3A634M9wIW4fiU433v/Lf/XvwjMAnvn7K9eN9T9wB9/PWf9/e/349vht/+18BGf5sXgDGxfOZ06/ot8AB0C/DNh+P8L78HgYuBz3RY/jXCJ2TXAbvbPL7G/yXPASqBxVGes+OX2Jl4f2Cm+o+P979wrgF6AVf5j0/wl68G/gPIBcbhfSlP85eV4/9x9h/39b+QhvmPC4CRkV6b/wXZABTj/YHI9eMd7T8eA+wGLvXXP83/InvEf67Rfjxtk6yDwOVAb+Cf8f5A9PaXv91h3Sa8P7w5wI+BP/rL+uD9ISvz9/MVvOSz7Zf5XuALEY75H4EfRHlPOjvmz+H9ofkc3lm254A7OxyDXm32NxTvDNzRwGfxvvAX+sty8P7oL/CPWW4o7nDvSZhYXwTu9vc9Ge+P3xEJWRfe+1je55/7r38s3lnks/zlc/AS3mGA+ctP8GN4F5jpxzQBLxEYGeZ1hf6pObNNWzVwpX+/Hjjfv/8ZYEKMv+PRXte1wNo2647wP0dHdxY78f+ujMD7Y/8FvM/zT/F+N0Kf/1l4n9PB/vPfBzwS4TWdAPytf8z64f2DsiKG3/lHgFvbxBv63HX2+a/C+wfoM3i/f1+M8F32d3j/MB4FzMBLcAo6+b75V//+VP/4TvBf/8+A59us6/ASz/7AKXjfMxdFOD7l/rG91I8lDzgbOMd/facBrwCzOux/aJvHE4D3gM/j/c5+Fe/76uhYPne6de0WeAC6BfwB8P57+xWwAziE95/ZSf6yI75E/PaLgINtHv+BT//gXuV/WfSO8HwXAIfxvvj3+V8Ey/n0v7VrgD932OZFP5aT8f7L7Ndm2Y+BX/n3yzkyIduL9+Wd12Gfkb4gH+rkeC0EFvj3T/PjH95m+U+AX7SJ549tlh1F+z+sb9M+IftDm3VHAI3+/cl4Sau1Wb6G2M+QvQ7cEGV5xGPu338OuK3Nsn8CnuhwDHpF2f+lwAb//rn+5+OI9SN93tosPwXvM9q3TduviZyQxfzex/g+tz0L82c+TZa2Al8Os48ZwP91aLsP+H6E5/xvYJ5//0y8BO0Y//E7wDeB42J5z2N8Xf3wkoZT/cc/BH4ZS+zE/7syjzYJFl4y1cynn/9X8P+x8h8X4CUVET9XbdYdB/zFvx/tfX8IuL/t+9jZ59+P4zAd/ln117mADmf7OyzfGPpchPvM0T4h+wXwkzbLjvVf/2n+Y0ebf7jwziDOjfC85bRJ5iKsMwt4rM3jjgnZfwJ3dNhmK34yqltybhpDluWcc684577mnBsMjML7D29hJ5sNwjutjpmdDEzB65YC+C3ef58lUbavc871d84dh/cfXyPeWTr859/eYf3t/nMWAh865z4Ksyzca9uP94flBqDezKrMbHgnr+3dtg/M7PNmtsrM9phZg7+vE6Nss92P84hlzrnDeIlv2+Vt7Wpz/wCQ64//KAR2Ov9bMVycnfgA7w9LJNGOeaTYjo20MzMbYGb/61+wsQ8v0Qgds5OB7c65Q7EG3yHOv/jva9s4jxDvex/j+xzpGJyMdwaxo1OBz5vZ3tANr9t0YIQwfo33Dw3A3+Od9TngP/5bvLOn281stZmdG+m1xPq6/N+jKrzuUvyfod/jWGKP53elkPa/CwfwPpchpwKPtXmuV/D++TopzGs6xszuM7Pt/ufreaC/meV08r5/F+8M5p/9K5yvaxNbpM//yXjfOX/pGEeYuK41s41tXsMojvwMRdIuBufcx3jHp0u/gxz53nzOzH5vZrv8Y/ajTmI7FfhOh/f/ZCJ/d0k3UEImrZxzr+L919ZxwH5HlwH/59+/Bu9zVGlmu/DGbuTidYfE8pwNeH+ISv2mOrwvg7ZOwTtDVAccb2b9wiwD77+8jvt/0jn3JbyE5FW8bqew60Zo/zXeWcOTnXP5wH/hfam3dXKHeOrCLTOzo/C6ZNouj0U9MMjM2j7vyZFWDuMPwGX+84cT7Zh3Jtxx/LHfPsZPuv+BT4/Zu8ApEQYaR3pPQuqBz3S4MvSUiIHF997H8j5H8i7hL454F1jt//MRuh3rnPtWhP08BZxoZuPwErNft3kt1c65LwMDgBV4Z0hi0dnregS4yk/w8oBVccQez+9KPd5nHwAzy8Pregx5F7i4w/PlOufCfQa/g9c9/Hn/8zU5tFuI/L4753Y5577hnCvEO9v4H/6VhdE+/+/ifef0DxNHKzM71X+eG/G6OvsDL7d5/Z19ttvF4H/GTyC238FwOj7ff+IdizP9Y/YvRP98vwv8sMP7cYxz7pEuxiMxUEKWxcxsuJl9x8wG+49PxvtD8Mcw6+aY2elm9jO8U/WhUhXX+vfHtbn9LVBiZid03E+Y/R6L95/5Zr9pJfA5M/t7M+tlZjPwuu9+75x7F29w6Y/NLNfMxgBf59P/6ncDp4USDzM7ycz+xv9y+wRvDEtLm3UHm1mfTkLsh/cfcpOZTcI7c9HR7f5/7SPxxtxUtFl2tpl9xU9AZvlxHHF8O/GiH/eN/jH5Mt4g3VjdjTde8EH/DwdmNsjM7vaPYcRjHsO+9+B16Qxp09YPf/CymQ3CG2MV8me8P853mllf/30s9pdFfU+cc9uBGuAHZtbHzL7Ap4l8O11472N5nyN5ALjDzM40zxj/s/97vON6jZn19m8TzeysCK/vEN5g7LvwxjU97b+WPmZ2tZnlO+cO4nX1Ry3tEcfrWomXCMzHG+R+2G+PK/YYnmsZUGpm5/nH/Qe0Twj+C/hhm8/nZ/3PeaTnacT7fB0PfD+0INr7bmZ/F/quwxsj5vxl0b5z6oHH8ZK3z/jHIZQAttXX398e/7lm0v4f286+b34NzDSzcWZ2NN4ZrD85596OsH68+uF9bj72zxh2/KdgN+1/h38O3GDeWU/zf1dLOvwzLN1MCVl2+whv0OafzGw/XqLwMt5/oCHnmtnHeL/Mz+H9YZ/onHvJzM7BG19zr//fZ+j2O7yrha4ivELz65DhnaY/Hq87BOfcB3hX93wH75T9d4G/ds697297lf+cdcBjeGNanvaXPer//MDM1uN9vr/jr/sh8EW88U/gXQW4GdhlZqF9h/NPwHwz+whvHEy4MxOr/df7DPBT59xTbZb9Fq8L5S94ZxO/4v9RjZlzrhlvIP/X8cbH/APeH8zW8iT+8Tw/wvYf4l1FdhDvvf7Ij7UBeCOGYx4ttgN4Y4/Wmte1cQ7eH9sJ/v6r8MYIhtZvwUuihuKNi9qBd3wgtvfk7/E+sx/i/SF+KMJ68b73sbzPkdztr/8U3u/JL/DGL30ETMf7h6MOr8vp3/AGbUfya7wrFh/t0K17DfC2ed1NN+B9BtoWw410pjDq63LOfYL3/vwV7c/IdSX2iM/lnNsM3AT8L15C/hHeoPHQZ3gR3tm1p/zt/4j3PoezEO9s3vv+ek+0WRbtfZ+I9/n/2H+uMufcWzF8/q/B+9151Y95VseAnHNbgH/H++dpN97FDWvbrBL1s+2cewbvytPf+MfnDD7tSu4O/4z3u/MRXrJV0WF5Od4/bHvN7ArnXA3eVZ/34H13vYE3Dk6SyNoPSxGRWJnZaXx61eQRY6LMrBxvoOw/JOG5/wT8l3NuSXfvWyTZ/DPje/G60N4KOByRlKAzZCJpwMy+aGYD/S6Vr+KVFXiis+1EUoWZlfpd+33xyl68hHelsYighEwkXQzDq9/VgNe1crk/vkUkXXwZryuxDq+sx5VOXTQirdRlKSIiIhIwnSETERERCZgSMhEREZGApfUs8CeeeKI77bTTgg5DREREpFPr1q173zn32XDL0johO+2006ipqQk6DBEREZFOmVnY6d5AXZYiIiIigVNCJiIiIhIwJWQiIiIiAUvrMWThHDx4kB07dtDU1BR0KFkhNzeXwYMH07t376BDERERSVsZl5Dt2LGDfv36cdppp2FmQYeT0ZxzfPDBB+zYsYPTTz896HBERETSVsZ1WTY1NXHCCScoGesBZsYJJ5ygs5EiIiIJyriEDIg7GZtx34vMuO/FJEWT2ZT4ioiIJC4jE7Kg7dq1iyuvvJIzzjiDESNGcMkll/Daa691aV8LFy7kwIEDXdp248aNrFy5skvbAtxzzz0MHToUM+P999/v8n5EREQkuqxPyFZs2MmGd/byp7c+pPjOZ1mxYWdC+3POcdlll3HBBRfw5ptvsmXLFn70ox+xe/fuLu0vyISsuLiYP/zhD5x66qld3oeIiIh0Li0TMjMrNbP7GxoaEtrPig07uWX5SzS3HAZg595Gbln+UkJJ2apVq+jduzc33HBDa9u4ceM4//zzcc4xZ84cRo0axejRo6moqADgueee44ILLuDyyy9n+PDhXH311TjnWLx4MXV1dUyZMoUpU6YA8K1vfYuioiJGjhzJ97///dbnqK6u5rzzzmPs2LFMmjSJhoYG5s2bR0VFBePGjaOiooLVq1czbtw4xo0bx/jx4/noo4+ivpbx48ejqalERESSLy2vsnTOVQKVRUVF30hkP3c9uZXGgy3t2hoPtnDXk1u5dPygLu3z5Zdf5uyzzw67bPny5WzcuJFNmzbx/vvvM3HiRCZPngzAhg0b2Lx5M4WFhRQXF7N27Vpuvvlm7r77blatWsWJJ54IwA9/+EOOP/54WlpamDZtGrW1tQwfPpwZM2ZQUVHBxIkT2bdvH8cccwzz58+npqaGe+65B4DS0lLuvfdeiouL+fjjj8nNzQW8hHHjxo1der0iIiKSuLQ8Q9Zd6vY2xtWeqDVr1nDVVVeRk5PDSSedxBe/+EWqq6sBmDRpEoMHD+aoo45i3LhxvP3222H3sXTpUiZMmMD48ePZvHkzW7ZsYevWrRQUFDBx4kQAjjvuOHr1OjLXLi4u5tvf/jaLFy9m7969resoGRMREQlWVidkhf3z4mqPxciRI1m3bl3YZc65iNsdffTRrfdzcnI4dOjQEeu89dZb/PSnP+WZZ56htraWkpISmpqacM7FdLXj3LlzeeCBB2hsbOScc87h1VdfjeEViYiISLJldUI258Jh5PXOadeW1zuHORcO6/I+p06dyieffMLPf/7z1rbq6mpWr17N5MmTqaiooKWlhT179vD8888zadKkqPvr169f61ivffv20bdvX/Lz89m9ezePP/44AMOHD6eurq71bNtHH33EoUOH2m0L8OabbzJ69Gi+973vUVRUpIRMREQkRWR1Qnbp+EH8+Cuj6ZPjHYZB/fP48VdGd3n8GHh1uR577DGefvppzjjjDEaOHEl5eTmFhYVcdtlljBkzhrFjxzJ16lR+8pOfMHDgwKj7u/7667n44ouZMmUKY8eOZfz48YwcOZLrrruO4uJiAPr06UNFRQU33XQTY8eO5Utf+hJNTU1MmTKFLVu2tA7qX7hwIaNGjWLs2LHk5eVx8cUXA94YsnAWL17M4MGD2bFjB2PGjOEf//Efu3xcREREJDKL1o2W6oqKilxNTU27tldeeYWzzjorrv2EisJWfPPcbostm3TlmIuIiKSCFRt2cteTW6nb20hh/zzmXDgsoRMz0ZjZOudcUbhlaXmVZXdTIiYiIpJ9QuWvQhUXQuWvgKQlZZFkdZeliIiIZK9o5a96ms6QiYiISFrrardjT5e/ikZnyERERCRthbodd+5txBHfrDvJKH/VVUrIREREJHArNuyk+M5nOX1uVVxzSyfS7ZiM8lddpS5LgCUl3s+ZVcHGISIikoUSGVyfSLdjaN89dZVlNDpDlgS7du3iyiuv5IwzzmDEiBFccsklvPbaa13a18KFCzlw4ECXtt24cSMrV67s0rYAV199NcOGDWPUqFFcd911HDx4sMv7EhERiSSRs1yJdjteOn4Qa+dO5a07S1g7d2ogyRgoIYPapbCjGravgQWjvMcJcM5x2WWXccEFF/Dmm2+yZcsWfvSjH7F79+4u7S/ohOzVV1/lpZdeorGxkQceeKDL+xIRkczX1W7HRM5ypVK3YyKyOyGrXQqVN0PLJ97jhne9xwkkZatWraJ3797ccMMNrW3jxo3j/PPPxznHnDlzGDVqFKNHj6aiogKA5557jgsuuIDLL7+c4cOHc/XVV+OcY/HixdTV1TFlyhSmTJkCwLe+9S2KiooYOXIk3//+91ufo7q6mvPOO4+xY8cyadIkGhoamDdvHhUVFa2V+levXs24ceMYN24c48ePbzetUjiXXHIJZoaZMWnSJHbs2NHl4yIiIpktqMH1oVl3BvXPw+ieWXeCkN1jyJ6ZDwc7ZN8HG732MVd0aZcvv/wyZ599dthly5cvZ+PGjWzatIn333+fiRMnMnnyZAA2bNjA5s2bKSwspLi4mLVr13LzzTdz9913s2rVKk488UQAfvjDH3L88cfT0tLCtGnTqK2tZfjw4cyYMYOKigomTpzIvn37OOaYY5g/fz41NTXcc889AJSWlnLvvfdSXFzMxx9/TG5uLuAljBs3boz4mg4ePMjDDz/MokWLunRMREQk80XrduwsOZpz4bB2Y8ggvrNcl44flHYJWEfZfYasIcIZn0jtCVqzZg1XXXUVOTk5nHTSSXzxi19snRB80qRJDB48mKOOOopx48bx9ttvh93H0qVLmTBhAuPHj2fz5s1s2bKFrVu3UlBQwMSJEwE47rjj6NXryFy7uLiYb3/72yxevJi9e/e2rhMtGQP4p3/6JyZPnsz555/f9RcvIiJpIYhux0w5y5WI7D5Dlj/Y66YM195FI0eOZNmyZWGXRZs39Oijj269n5OTw6FDh45Y56233uKnP/0p1dXVfOYzn+FrX/saTU1NOOcws05jmzt3LiUlJaxcuZJzzjmHP/zhDwwfPjzqNj/4wQ/Ys2cP9913X6f7FxGR9JbI1Y6F/fPYGSb5imdwfTYlYB1l9xmyafOgd4cPSu88r72Lpk6dyieffMLPf/7z1rbq6mpWr17N5MmTqaiooKWlhT179vD8888zadKkqPvr169f61ivffv20bdvX/Lz89m9ezePP/44AMOHD6eurq71bNtHH33EoUOH2m0L8OabbzJ69Gi+973vUVRUxKuvvhr1uR944AGefPJJHnnkEY46Krs/KiIi2SBTanqlo7T8K2tmpWZ2f0NDQ2I7GnMFlC6GHP/sVP7J3uMujh/zY+Oxxx7j6aef5owzzmDkyJGUl5dTWFjIZZddxpgxYxg7dixTp07lJz/5CQMHDoy6v+uvv56LL76YKVOmMHbsWMaPH8/IkSO57rrrKC4uBqBPnz5UVFRw0003MXbsWL70pS/R1NTElClT2LJlS+ug/oULFzJq1CjGjh1LXl4eF198MeCNIQvnhhtuYPfu3Zx77rmMGzeO+fPnd/m4iIhIz1G3Y/qxaN1oqa6oqMjV1NS0a3vllVc466yz4tuRCsMmpEvHXEREkqJjtyN4Z6piSY6K73w2bLfjoP55rJ07tdtjzTZmts45VxRuWVqeIet2M6uUjImISErJ9qmEsk12D+oXERFJQZpKKPsoIRMREUkxidT00tWO6UldliIiIkmiqYQkVjpDJiIikgRB1fRSt2N6UkIGzHxiJgBLLloScCQiIpIpNJWQxENdlkmwa9currzySs444wxGjBjBJZdcwmuvvdalfS1cuJADBw50aduNGzeycuXKLm0L8PWvf52xY8cyZswYLr/8cj7++OMu70tEJF2pppf0hKxPyKq2VVG7p5aa3TVMXzadqm2Jlb9wznHZZZdxwQUX8Oabb7JlyxZ+9KMfsXv37i7tL8iEbMGCBWzatIna2lpOOeWU1knKRUSyRajbcefeRhyfdjvGkpRF6l6MZ3D92rlTeevOEtbOnapkLMNldUJWta2K8hfKaT7cDED9/nrKXyhPKClbtWoVvXv35oYbbmhtGzduHOeffz7OOebMmcOoUaMYPXo0FRUVADz33HNccMEFXH755QwfPpyrr74a5xyLFy+mrq6OKVOmMGXKFAC+9a1vUVRUxMiRI/n+97/f+hzV1dWcd955jB07lkmTJtHQ0MC8efOoqKhordS/evVqxo0bx7hx4xg/fny7aZXCOe644wAvyWxsbIxpvkwRkUyiml5ZoHYpLBgF5f29n7VLAwkjq8eQLVq/iKaWpnZtTS1NLFq/iJIhJV3a58svv8zZZ58ddtny5cvZuHEjmzZt4v3332fixIlMnjwZgA0bNrB582YKCwspLi5m7dq13Hzzzdx9992sWrWKE088EYAf/vCHHH/88bS0tDBt2jRqa2sZPnw4M2bMoKKigokTJ7Jv3z6OOeYY5s+fT01NTeuZrdLSUu69916Ki4v5+OOPyc3NBbyEcePGjWFjnjlzJitXrmTEiBH8+7//e5eOiYhI0FZs2NmlQe6q6ZXhapdC5c1w0H8/G971HkNC0yh2RVafIdu1f1dc7Ylas2YNV111FTk5OZx00kl88YtfbJ0QfNKkSQwePJijjjqKcePG8fbbb4fdx9KlS5kwYQLjx49n8+bNbNmyha1bt1JQUMDEiRMB78xWr15H5trFxcV8+9vfZvHixezdu7d1nUjJGMCSJUuoq6vjrLPOaj2jJyKSTtTtKBE9M//TZCzkYKPX3sOyOiEb2Df8xN6R2mMxcuRI1q1bF3ZZtHlDjz766Nb7OTk5HDp06Ih13nrrLX7605/yzDPPUFtbS0lJCU1NTTjnYupOnDt3Lg888ACNjY2cc845vPrqqzG8Ii+eGTNm8Jvf/Cam9UVEUom6HbNAV7sdG3bE155EWZ2QlU0oIzcnt11bbk4uZRPKurzPqVOn8sknn/Dzn/+8ta26uprVq1czefJkKioqaGlpYc+ePTz//PNMmjQp6v769evXOtZr37599O3bl/z8fHbv3s3jjz8OwPDhw6mrq2s92/bRRx9x6NChdtsCvPnmm4wePZrvfe97FBUVRU3InHO88cYbrfcrKysZPnx41w6KiEiAdLVjhgt1Oza8C7hPux1jScryB8fXnkRZPYYsNE5s3tp5NB9upqBvAWUTyro8fgzAzHjssceYNWsWd955J7m5uZx22mksXLiQyZMn8+KLLzJ27FjMjJ/85CcMHDgwamJ0/fXXc/HFF1NQUMCqVasYP348I0eOZMiQIRQXFwPQp08fKioquOmmm2hsbCQvL48//OEPTJkyhTvvvJNx48Zxyy23sGbNGlatWkVOTg4jRozg4osvBsKPIXPO8dWvfpV9+/bhnGPs2LH853/+Z5ePi4hIoro6DkxTCWW4aN2OnY0Dmzav/RgygN55XnsPs2jdaKmuqKjI1dTUtGt75ZVXOOuss+LajwrDJqYrx1xEJB4dq96D13UYy9mqRLaVNFDeHwiXyxiU7+18+9qlXvLWsMM7MzZtXtIG9JvZOudcUbhlWX2GLESJmIhIakuk6r2udkwTXU2M8gf73ZVh2mMx5ooev6IyHCVkIiLSo7rS9ZjIODBQt2PKS6T8RAp1OyYiqwf1i4hIz+pqCYpEy09Iikuk/MSYK6B0MeSfDJj3s3RxSpz1iofOkImISI/patdjopNtS4pLtPxEinQ7JkJnyEREpMd0tetR5SfSRFfrgaVQ+Ymg6AwZsP2aawE49eGHAo5ERCQ9BFGCQuPAUpzGgSVEZ8iSYNeuXVx55ZWcccYZjBgxgksuuYTXXnutS/tauHAhBw4c6NK2GzduZOXKlV3atq2bbrqJY489NuH9iEhmSGQqIlW+z2AaB5aQrE/IGiorady0iQPV1bw+dRoNlZUJ7c85x2WXXcYFF1zAm2++yZYtW/jRj37E7t27u7S/oBOympoa9u7dm9A+RCSzJDIVkboe00BQ0xCNuQJmv+zVDpv9clYlY5DlXZYNlZXU3z4P19wMwKG6Oupv906P5peWdmmfq1atonfv3txwww2tbePGjQO8ZO273/0ujz/+OGbGbbfdxowZM3juuecoLy/nxBNP5OWXX+bss8/mv//7v/nZz35GXV0dU6ZM4cQTT2TVqlV861vforq6msbGRi6//HJ+8IMfAN70TGVlZezfv5+jjz6ap59+mnnz5tHY2MiaNWu45ZZbGDhwIGVl3rRQZsbzzz9Pv379Ir6WlpYW5syZw69//Wsee+yxLh0PEck8KkGRwRLpdky0HliWy+qE7L0FC3FNTe3aXFMT7y1Y2OWELJRQhbN8+XI2btzIpk2beP/995k4cSKTJ08GYMOGDWzevJnCwkKKi4tZu3YtN998M3fffTerVq3ixBNPBOCHP/whxx9/PC0tLUybNo3a2lqGDx/OjBkzqKioYOLEiezbt49jjjmG+fPnU1NTwz333ANAaWkp9957L8XFxXz88cfk5nrzeIabOgngnnvu4W/+5m8oKCjo0rEQkdQW1FREksIyZBqidJTVXZaH6uvjak/UmjVruOqqq8jJyeGkk07ii1/8YuuE4JMmTWLw4MEcddRRjBs3jrfffjvsPpYuXcqECRMYP348mzdvZsuWLWzdupWCggImTpwIwHHHHUevXkfm2sXFxXz7299m8eLF7N27t3WdcMlYXV0djz76KDfddFP3vHgRSSkaByZhJdLtqHFgCcnqhKxXhDM/kdpjMXLkSNatWxd2WbR5Q48++ujW+zk5ORw6dOiIdd566y1++tOf8swzz1BbW0tJSQlNTU045zCzTmObO3cuDzzwAI2NjZxzzjlRJzXfsGEDb7zxBkOHDuW0007jwIEDDB06tNPnEJH0oHFgGS6o8hNZPg4sEVmdkA2YPQvzu+1CLDeXAbNndXmfU6dO5ZNPPuHnP/95a1t1dTWrV69m8uTJVFRU0NLSwp49e3j++eeZNGlS1P3169ePjz76CIB9+/bRt29f8vPz2b17N48//jgAw4cPp66urvVs20cffcShQ4fabQvw5ptvMnr0aL73ve9RVFQUNSErKSlh165dvP3227z99tscc8wxvPHGG10+LiKSWrpjHNjauVN5684S1s6dqmQslYTGgTW8C7hPx4HFkpRNm+d1M7albscekTIJmZmNMLOlZvafZnZ5TzxnfmkpBXfMx/r0AaBXYSEFd8zv8vgx8AbLP/bYYzz99NOcccYZjBw5kvLycgoLC7nssssYM2YMY8eOZerUqfzkJz9h4MCBUfd3/fXXc/HFFzNlyhTGjh3L+PHjGTlyJNdddx3FxcUA9OnTh4qKCm666SbGjh3Ll770JZqampgyZQpbtmxh3LhxVFRUsHDhQkaNGsXYsWPJy8vj4osvBj696EBE0s+KDTspvvNZTp9bRfGdz8bU5QiaiiijqfxEWrJo3WgJ79zsl8BfA+8550a1ab8IWATkAA845+40s+8Af3bO/Z+Z/c459zed7b+oqMjV1NS0a3vllVc466yz4opThWET05VjLiKJC40D6zidUCzdh4lsKymuvD8Q7m+7eV2JEhgzW+ecKwq3LNlnyH4FXNQhmBzgXuBiYARwlZmNAB4GrjSzu4ATkhxXO6c+/JCSMRFJOxoHJmFpGqK0lNSyF865583stA7Nk4A3nHPbAMzsf4EvO+d+DPw/P2Fbnsy4REQygeqBZbjapV43Y8MOL5maNi+2rkOVn0hLQdQhGwS0rRy3A/i8n7j9C9AXuCvSxmZ2PXA9wCmnnJK8KEVEeojqgckREinQGlrelWQuC1Vtq2LR+kXs2r+LgX0HUjahjJIhJT0eRxAJWbj6DM459zZ+ohWNc+5+4H7wxpBFWCemMhCSuGSOQRTJBh3HcoXqgQGdJmVzLhwWdhyY6oFlgEQKtIK3jhKwTlVtq6L8hXKaWrwi8fX76yl/oRygx5OyIK6y3AGc3ObxYKCuu3aem5vLBx98oEShBzjn+OCDD1or/otI/DQOTMJKdF5Iicmi9Ytak7GQppYmFq1f1OOxBHGGrBo408xOB3YCVwJ/3107Hzx4MDt27GDPnj3dtUuJIjc3l8GDNVBUpKs0DkzC0ryQPWLX/l1xtSdTUhMyM3sEuAA40cx2AN93zv3CzG4EnsQre/FL59zm7nrO3r17c/rpp3fX7kREkkrjwDKcBub3iK6OAxvYdyD1+4+cLnFg3+g1QpMhqV2WzrmrnHMFzrnezrnBzrlf+O0rnXOfc86d4Zz7Ybz7NbNSM7u/oaGh+4MWEemCrhZo1byQGSyRivkq0Bqz0Diw+v31OFzrOLCqbVWdbls2oYzcnPbDbnJzcimbUJascCNKamHYZAtXGFZEpKclWmS1q1dZSopbMCpCt+PJ3jyP0i2mL5se9ixXQd8Cnrr8qU6378mrLKMVhg1iDJmISEaJNjA/lsRK48AylAbm94hEx4GVDCkJpMxFRykzl6WISLpKdGC+ZChVzO8RkcZ7BTEOLBFKyEREfJqoW8KqXep1P5b3937GMgYMvAH4vTt8BjQwP6KqbVVMXzadMQ+OYfqy6TGNAYPUGgeWiLRMyDSoX0S6W2gc2M69jTg+LdAaS1KmgfkZTAPze0QiA/NLhpRQfl45BX0LMIyCvgWUn1eeEt2Q8dCgfhERoPjOZ8OWnxjUP4+1c6d2ur0G5mcoDczvEYkOzE8XGtQvItIJFWiVsDQwv0ekUoHWoKRll6WISHfTODAJSwPze0SmDMxPhBIyERE0Dkwi0MD8uGT7wPxEqMtSRDJKV8dyhdbROLAM1dUpjELrdGXbLBMamB+arDs0MB/odIB9aHlPFWhNRRrULyIZI9GK+ZKhQldKdpwXUlc8dqtsGZifiGiD+tOyy1JlL0QknGgV8yWLPTO/fTIG3uNn5gcTT4bSwPzEpGVC5pyrdM5dn5+fH3QoIpJCVDFfwtKVkj1CA/MTk5YJmYhIOLpSUsLSlZJx0cD8YCghE5GMoSslM5ymMEo6VcwPjgb1i0jKSaTqvSrmZ6hEB+Z39SrLLKOB+ckVbVC/EjIRSSm6UlLC0hRGPWLMg2NwHJkXGEbtV2sDiCizZNxVliKSuXSlpISlgfk9QgPzg5OWCZnKXohkLl0pKWFpYH6P0MD84KRlQqayFyKZS1dKSlgamB+Xrl4pmY0D8xsqK3l96jReOWsEr0+dRkNlZSBxaOokEUkpcy4cFnYMma6UzCBdGWCvKYxilsgURqF1MjkBa6uhspL62+fhmrxjdaiujvrbvSQ/v7S0R2PRoH4RSQpdKSlhaRqjpNOVkrF7feo0DtXVHdHeq7CQM599ptufL9qgfp0hE5Fu1/FKyZ17G7ll+UsAMU/0rQQsQ0WbxkgJWbfQFEaxO1R/ZOIarT2Z0nIMmYikNl0pKRHpasmk05WSsetVUBBXezIpIRORbqcrJSUiXS2ZdNl4pWRXB+YPmD0Ly21/rCw3lwGzZyUhyuiUkIlIt9OVkhKRrpZMumy7UjI0MP9QXR041zowP5akLL+0lII75tOrsBDM6FVYSMEd83t8QD9oUL+IJIGq7UtUmsYoJlXbqli0fhG79u9iYN+BlE0oy9ikKhE9PTA/ERk3qN/MSoHSoUOHBh2KiIQRSrp0pWQGSySpGnOFErBOJFq6Ipuk0sD8ROgMmYhEpPITEpZKVySdSlfELlPOkGkMmYiEFep23Lm3EcenpStWbNgZdGgStGilK6RbqHRF7FJpYH4ilJCJSFgqXSERqXRF0mVj6YquXimZSgPzE5GWY8hEJPlUukIiyh8MDe+Gb5duUTahrN0YMsjs0hWJTmGUX1qadglYRzpDJiJhqXSFRKTSFUmXbaUr3luwsDUZC3FNTby3YGEwAQVAZ8hEJCxN8i0RaaLvmCVSuiKbJvnOlCslE6GETETCUukKiUqlKzql0hWx61VQEP5KyQCmMAqKEjKRDJdI6QpN8p3hVKA1qRatX9RuDBhAU0sTi9YvUkLWwYDZs9qNIYP0vFIyERpDJpLBVLpCIgrVEmt4F3Dez8qbvXbpFtlYuiLbr5RMhM6QiWSwaKUrdOYry0WrJaazZN1iYN+BYYu7ZmrpCl0pmZi0PENmZqVmdn9DQ0PQoYikNJWukIhUSyzpyiaUkZvTvmBpJpeu0JWSiUnLhMw5V+mcuz4/Pz/oUERSmkpXSESRaoaplli3ybbSFbpSMjHqshTJYCpdIRFNmxd+PkrVEjuCSlfERldKJiYtz5CJSGwuHT+IH39lNIP652HAoP55/PgrozV+TLxxYqWLIf9kwLyfmhz8CKHSFfX763G41tIVVduqgg4t5WTKnJJBMedc0DF0WVFRkaupqQk6DJEekUj5ChHpmunLpocdmF/Qt4CnLn8qgIhSW0NlJe8tWMih+np6FRQwYPasrB6o35GZrXPOFYVbpi5LkTQQKl8R6noMla8AlJRlO9USS6psLV3R1aQq26+UTIS6LEXSQLTyFZLFVEss6SKVqMj00hWH6urAudbSFbHWE5OuU0ImkgZUvkLCilZLTLqFSleodEVPUZelSBoo7J/HzjDJl8pXZDnVEku60BWSXb3KMt2odEVwlJCJpAGVr5Cw8gf73ZVh2qUdla6IjUpXBEddliJpQOUrJKxp87zaYW2pltgRVLoidipdERyVvRARSWe6yrJT2Vi6oqGykvpbb8M1N9OrsDCuKyVVuiJ5VPZCRCRTjblCCVgnsq10Resk383NgCb5ThfqshTpQSs27KT4zmc5fW4VxXc+y4oNO4MOSSTjZVvpCl0pmZ7SMiEzs1Izu7+hoSHoUERiFiruunNvI45Pi7sqKRNJrmwrXaErJdNTWiZkzrlK59z1+fn5QYciEjMVdxUJRsmQEsrPK6egbwGGUdC3gPLzyjP2yslIV0TqSsnUpjFkIj1ExV0lotql8NsboeUTb5JvDczvdtlUumLA7FneGLI23Za6UjL1peUZMpF0FKmIq4q7ZrnQ9Ectn3iPNf1RRFXbqpi+bDpjHhzD9GXTVbYigvzSUgrumE+vwkIwo1dhIQV3zNdA/RSnhEykh8y5cBh5vXPatam4q2j6o9hkYy2xhspKXp86jVfOGsHrU6fFNZ9kfmkpZz77DGe9soUzn31GyVgaUEIm0kNU3FXC0vRHMVm0fhFNLe2vHGxqaWLR+kUBRZRcmuQ7+2gMmUgPunT8ICVg0p6mP4pJttUSi1a6Qme7MpPOkImIBEnTH8Uk22qJqXRF9lFCJiISpDFXQOli7+pKzPtZulhXWXaQbbXEVLoi+6jLUiROKzbs5K4nt1K3t5HC/nnMuXCYuiElMZr+qFOhkhWL1i9i1/5dDOw7kLIJZRlbykKlK7JP1ITMzHKBvwbOBwqBRuBloMo5tzn54YmkllC1/VCB11C1fUBJmUiSpWMtsa5O8h1aR5N8Zw9zzoVfYFYOlALPAeuA94Bc4HPAFP/+d5xztT0RaDhFRUWupqYmqKeXLFR857PsDFPIdVD/PNbOnRpARJIyapd6pSoadngD8lXcNeu1TvLd4SyXaoJlLzNb55wrCrcs2hmyaudceYRld5vZAOCURIMTSSeqti9hhYq7huqJhYq7gpKyLKYrJSUeEQf1O+eiVttzzr3nnNPpKckqqrYvYam4a1yqtlVx9sNnM/rB0RldcV9XSko8unSVpZnd392BiKQDVduXsFTcNWahivvNh5sBMrrivq6UlHhETMjM7PgItxOAS3owRpGUoWr7ElakIq4q7nqEbKq4P2D2LCy3fakOXSkpkUQbQ7YH2A5YmzbnPx6QzKBEUpmq7csRps1rP4YMVNw1gmyquK8rJSUe0RKybcA059w7HReYWZh5PkREslRo4L6usuzUwL4Dqd9/5BiqTK24n19aqgRMYhItIVsIfAY4IiEDfpKUaERE0pWKu8akbEIZ5S+Ut+u2zOSK+yKxipiQOefujbLsZ8kJR6RnrNiwk+8uq6W55TCDVG1fpMekY8X9rhZ3FYlHxMKwYVc2u985d30S44k1jlKgdOjQod94/fXXgw5H0kzHavvgXSmpwfki0pGKu0p3ilYYNt6yF2F30tOcc5XOuevz8/ODDkXS0F1Pbm2XjAE0Hmzhrie3BhSRiKSqaMVdRbpTvAnZe0mJQqQHqdq+RFS7FO4YAOX5sGCU91jCUnFXFXeV7hVvQnaJmR2XlEhEeoiq7UtYoemPWj7xHoemP1JSdgQVd1VxV+l+nSZkZvZrMzvOzPoCW4CtZjYn+aGJJIeq7UtYmv4oZiruquKu0v1iOUM2wjm3D7gUWIk3ofg1yQxKJJlUbV/C0vRHMcu24q4Fd8ynV2EhmNGrsFAD+iUpotUhC+ltZr3xErJ7nHMHzSz2SzNFUpCq7csR8gd73ZTh2qUdFXcV6X6xnCG7D3gb6As8b2anAvuSGZSISI+bNs+b7qgtTX8UVtmEMnJz2nfjqbirSGI6PUPmnFsMLA49NrN3gCnJDEpEpMdp+qOYpWNxV4Dt11wLwKkPPxRwJCJHiqswbKopKipyNTU1QYchIiIpTtX2JRV0Z2FYERGRtNJabb/ZK9NxqK6O+tvn0VBZGXBkIp9SQiZpbcZ9LzLjvheDDkNSzZIS7yaCqu1LeuhSQmZmX+ruQETitWLDTja8s5c/vfUhxXc+y4oNO4MOSVJB7VLYUQ3b16javgCqti/poatnyH7RrVGIxCk0QXhzy2EAdu5t5JblLykpy3aqth+3mU/MZOYTM4MOI6lUbV/SQcSEzMx+F+FWCZzQgzGKHEEThEtYqrYfl6ptVdTuqaVmd01Gz0epavuSDqKVvTgf+Afg4w7tBkxKWkQiMdAE4RKWqu3HLNJ8lEDKl6+IV+hqyvcWLORQfT29Cgp0laWknGgJ2R+BA8651R0XmJlOQ0igCvvnsTNM8qUJwrOcqu3HLNp8lKmckHW1lpiq7Uuqi9hl6Zy72Dm3KsKyyckLSaRzmiBcwlK1/Zil43yUDZWVNG7axIHqal6fOk1lKySjxDWo38z+OlmBiMRDE4RLWGOugNLFkH8yYN7P0sWqth9GpHknU3U+StUSk0wXV6V+M1vvnJuQxHjiokr9IiJdExpD1rbbMjcnl/LzylOyy/L1qdM4VFd3RHuvwkLOfPaZACISiV+0Sv2dzmXZcV/dEI+IiAQs3eajVC0xyXTxJmTfTEoUIiLS40qGlKRsAtZRr4KC8GfIVEtMMkTEhMzMvhKhfTCAc255soISERFpa8DsWd4YsjZTIKmWmGSSaGfIlgEb/Ru07650gBIyEZEUEKq0v+SiJQFHkjyhkhX1t96Ga26mV2GhaolJRomWkP0tMAMYA/wWeMQ590aPRCUiIjEJVdtvPtzM9GXTU3ocWKLyS0vZu/RRIP46ZCKprtOrLM2sL/BlvOTsBODWcMVig6CrLEUy2BI/qZiZmdP5dId0u1Kyra4WeBVJZ9GusoylDlkT0ADsA/oCudFXFxFJUO1S2FEN29fAglGaHDyCaNX2U5kKvIocKdqg/inAVXjzVv4BWOSc0+ko6XYz7nsRgIpvnhtwJJISapdC5c3Q8on3uOFd7zGowGsH6VptP1yBV0DjwSSrRTtD9gxeMrYGOBq41swWh249Ep1kvBUbdrLhnb386a0PKb7zWVZs2Bl0SBK0Z+bDwQ7zlB5s9NqlnXSrtg/eBN9tr5QEcE1NvLdgYTABiaSIaIP6r8O7mlIkKVZs2Mkty1+iueUwADv3NnLL8pcANAVSNmvYEV97FiubUBZ2DFnZhLIAo4pOBV5FwouYkDnnftWDcWBmpwD3AO8Drznn7uzJ55eed9eTW2k82NKurfFgC3c9uVUJWTbLH+x1U4Zrl3ZCA/fnrZ1H8+FmCvoWpPxVlirwKhJexC5LM7vfzEZFWNbXzK4zs6uj7dzMfmlm75nZyx3aLzKzrWb2hpnN9Zs/B1Q5564DRsT5OiQN1e1tjKtdssS0edA7r31b7zyvXY5QMqSEddes46WvvsRTlz+V0skYeAVeLbf9tWEq8CoSfQzZfwDzzOwVM3vUzP7DT7D+D3gB6IdXPDaaXwEXtW0wsxzgXuBivMTrKjMbAWwArjSzZ4FVXXo1klYK++fF1S5ZYswVULoYco72Huef7D3WgP6MkF9aSsEd87E+fQBvcvCCO+ZrQL9kvWhdlhuBK8zsWKAIKAAagVecc1tj2blz7nkzO61D8yTgDefcNgAz+1+8OmcHge/72ywDMrfktAAw58Jh3LL8pXbdlnm9c5hz4bAAo5KUMOYKJWAZTAVeRY7U6eTizrmPgee68TkHAW0HiOwAPg/8F1BuZn8PvB1pYzO7Hrge4JRTTunGsKSnhcaJfXdZLc0thxnUP485Fw7T+DHJSuk4/VEixV2ViIm012lClgQWps05514GLu9sY+fc/cD94FXq7+bYpIddOn4Qj/z5HUB1yEREJHvFUqm/u+0ATm7zeDBw5CU3kjUqvnmukrFMtaTk0ymQJKLQfJQ1u2uYvmw6VdtSf7ooVdsX6V4xJ2T+nJbdoRo408xON7M+wJXA77pp3yIiaSU0H2XzYa9yff3+espfKE/ppCxStX0lZSJd12lCZmbnmdkW4BX/8Vgz+49Ydm5mjwAvAsPMbIeZfd05dwi4EXjS3+dS59zmLr8CEUlNmo8yJuk4H6Wq7Yt0v1jGkC0ALsQ/i+Wc22Rmk2PZuXPuqgjtK4GVsQbZkZmVAqVDhw7t6i5EJJk0H2XM0nE+SlXbF+l+MXVZOuc6ls1uCbtiD3HOVTrnrs/Pzw8yDBGJRPNRxiwd56OMVFVf1fZFui6WhOxdMzsPcGbWx8z+Gb/7UkQkLM1HGbOyCWXk5rSvXJ/q81Gq2r5I94uly/IGYBFe/bAdwFPAPyUzKBFJc5qPMmbpOB9lqKp+/a234Zqb6VVYyIDZs1RtXyQBsSRkw5xz7easNLNiYG1yQhKRtDdtnjdmrG23peajjKhkSAnLXvNmokuXwrCqti/Svcy56LVVzWy9c25CZ209qc2g/m+8/vrrQYUhItHULoXf3ugN7M8/2UvGNKBfRLKYma1zzhWFWxbxDJmZnQucB3zWzL7dZtFxQE73hhgf51wlUFlUVPSNIOMQkSjGXAHrHvTuz0zdmlrdKdumPxKR7hOty7IPcKy/Tr827fuIYYojEZFsScRERBIVMSFzzq0GVpvZr5xz23swJhGRtBOa/qj5cDPTl01P+YH5IpJaYhnUf8DM7gJGAq3XOTvnpiYtKkk7M+57EdAE4RkpNBelznZFFGn6IyClk7LQfJSuuZnXp07TlZIiAYqlDtn/AK8CpwM/AN7Gm49SRERIz+mPNB+lSGqJJSE7wTn3C+Cgc261c+464JwkxyVpZMWGnWx4Zy9/eutDiu98lhUbdgYdknQXzUcZk3Sc/kjzUYqkllgSsoP+z3ozKzGz8UCg1R3NrNTM7m9oaAgyDMFLxm5Z/hLNLYcB2Lm3kVuWv6SkLBNEmo9SSdkR0nH6I81HKZJaYknI/tXM8oHvAP8MPADMTmpUndBclqnjrie30niw/dSmjQdbuOvJrQFFJN1G81HGLB2nP9J8lCKpJWpCZmY5wJnOuQbn3MvOuSnOubOdc7/rofgkxdXtbYyrXdKI5qOMWcmQEsrPK6fPUX0AKOhbQPl55Sk9oF/zUYqklqgJmXOuBfibHopF0lBh/7y42iWNRJp3UvNRhlUypIQxnx1D0UlFPHX5UymdjIE39VHBHfOxPl4S2auwkII75usqS5GAxNJl+YKZ3WNm55vZhNAt6ZFJWphz4TDyerefuCGvdw5zLhwWUETSbabN8+afbEvzUWaU/NJS8saO5ZiJEznz2WeUjIkEKJa5LFeFaXapUIesqKjI1dTUBB1G1luxYSffXVZLc8thBvXPY86Fw7h0/KCgw5LuoPkoRUS6TZfmsgxxzk3p/pAkk1w6fhCP/PkdQIVhM47moxQR6RGxVOpPOWZWCpQOHTo06FBEMl+WJGLpTBOEi6S/WMaQpRyVvUg9Fd88V2fHJO2F5qOs2V3D9GXTqdqmZFREekZaJmQiIt0t0nyUqZ6UheajPFBdzetTp2nqI5E0FVOXpZmdB5zWdn3nnM6Ni0jGiDYfZaqWsIg0HyWgKyZF0kynZ8jM7GHgp8AXgIn+LewVAiIi6UrzUYpIkGI5Q1YEjHCd1ccQEUljA/sOpH7/kfM4aj5KEekJsYwhexlI3W8kEZFuoPkoRSRIsSRkJwJbzOxJM/td6JbswESkGy0p8W4SkeajFJEgxdJlWZ7sIEREUkHJkBKWvbYMSI/CsKGB+/W33oZrbqZXYSEDZs/SgH6RNBRLpf7VZnYS3mB+gD87595LbljRqTCsiIgnv7SUvUsfBVQYViSdxXKV5RXAn4G/A64A/mRmlyc7sGhUGFYkDrVLYUc1bF8DC0Z5jyWiJRctCeTs2PZrrm2tuC8i2SeWLstbgYmhs2Jm9lngD8CyZAYmIt2gdilU3uxNDg7Q8K73GDRJuIhICoklITuqQxflB6jCv0h6eGY+HGxs33aw0WtXQpYx1FUpkv5iSaye8K+w/JqZfQ2oAlYmNywR6RYNO+Jrl0Bo+iMRiWVQ/xwz+1ugGDDgfufcY0mPTHrcjPteBNAk4Zkkf7DXTRmuPYPNfGImkB5XSmr6IxGBGLsenXO/cc592zk3W8mYSBqZNg9657Vv653ntUtK0PRHIgJREjIzW+P//MjM9rW5fWRm+3ouRBHpsjFXQOliyDnae5x/svdY48dShqY/EhGIkpA5577g/+znnDuuza2fc+64ngtResKKDTvZ8M5e/vTWhxTf+SwrNuwMOiTpLmOugMET4dQvwOyXMz4Zq9pWRe2eWmp21zB92XSqtlUFHVJUmv5IRCC2OmQPx9Im6WvFhp3csvwlmlsOA7BzbyO3LH9JSZmknaptVZS/UE7zYW88Vv3+espfKE/ppEzTH4kIxDaGbGTbB2bWCzg7OeFIEO56ciuNB1vatTUebOGuJ7cGFJFI1yxav4imlvbjsZpamli0flFAEXUuv7SUgjvmY328OTR7FRZScMd8DegXyTIRr7I0s1uAfwHy2owZM6AZuL8HYotIUyd1r7q9jXG1SxqambpniLrTrv274mpPFZr+SESijSH7sXOuH3BXh/FjJzjnbunBGMPFpqmTulFh/7y42kVS1cC+A+NqFxFJFZ12WTrnbjGzz5jZJDObHLr1RHDSM+ZcOIy83jnt2vJ65zDnwmEBRSTi1RIL1ROLVdmEMnJz2o/Hys3JpWxCWXeGlhSnPvyQzo6JZLFOC8Oa2T8CZcBgYCNwDvAiMDWpkUmPuXT8IAC+u6yW5pbDDOqfx5wLh7W2i6SLkiElAMxbO4/mw80U9C2gbEJZa7uISKqKZS7LMmAi8Efn3BQzGw78ILlhSU+7dPwgHvnzO4Aq9Ut6KxlSwrLXlgHpUalfRARiu8qyyTnXBGBmRzvnXgXUlyUShCUl3k1ERDJKLAnZDjPrD6wAnjaz3wJ1yQxKRLJbuhV3FRFJVCyTi1/m3y03s1VAPvBEUqOSQKirUlJBpOKuQMxjwdRVKSLpJtpclsf5P48P3YCXgDXAsT0Un4iE1C6FHdWwfQ0sGOU9zkDpWNw1ZPs117L9mmuDDkNE0lC0M2S/Bv4aWAc4vKKwbX8OSXp0IuKpXQqVN0PLJ97jhne9x5Bxc1Oma3FXEZFERCsM+9f+z9Odc0M6/uy5EEWEZ+bDwQ4zJxxs9NozjIq7ikg2imVy8cvMLL/N4/5mdmlSoxKR9hp2xNeextK5uKuISFfFcpXl951zDaEHzrm9wPeTFpGIHCl/cHztaaxkSAnl55XT5yhvsu2CvgWUn1eu4q4iktFiScjCrRNLQVkR6S7T5kHvDnOL9s7z2jNQyZASxnx2DEUnFfHU5U+lRTLWUFlJ46ZNHKiu5vWp02iorAw6JBFJI7EkZDVmdreZnWFmQ8xsAd5A/8CYWamZ3d/Q0ND5yiKZYMwVULoYco72Huef7D3OsAH96aqhspL62+fhmr1SHYfq6qi/fZ6SMhGJWSwJ2U1AM1ABPAo0Af8vmUF1xjlX6Zy7Pj8/v/OVRTLFmCtg8EQ49Qsw+2UlYynkvQULcU3tS3W4pibeW7AwmIBEJO3EUhh2PzDXr0t22Dn3cfLDEpFsl07FXQ/V18fVLiLSUSxXWY42sw14RWE3m9k6MxuV/NBERNJDr4KCuNpFRDqKpcvyPuDbzrlTnXOnAt8B7k9uWCIS1swq7yYpZcDsWVhu+1IdlpvLgNmzgglIRNJOLFdL9nXOrQo9cM49Z2Z9kxiTiEhayS8tBaD+1ttwzc30KixkwOxZre0iIp2JJSHbZma3Aw/7j/8BeCt5IYmIpJ/80lL2Ln0UgFMffijgaEQk3cTSZXkd8FlgOfAYcCIwM5lBiYiIiGSTWK6y/AtwM4CZ5eB1Ye5LdmAiIiIi2SKWqyx/bWbH+ePGNgNbzWxO8kMTkXQ384mZzHxCJ9RFRDoTyxiyEc65fWZ2NbAS+B5epf67khqZiEia0dgxEemqWMaQ9Taz3sClwG+dcwcBl9SoRDLZkhLvJiIi4ou1DtnbQF/geTM7FdAYMhEREZFu0mlC5pxb7Jwb5Jy7xHm2A1N6IDYRSWNV26qo3VNLze4api+bTtU2FbQVEYkklkH9Zf6gfjOzX5jZemBqD8QmImmqalsV5S+U03y4GYD6/fWUv1CupExEJIKY6pD5ZS6m49UjmwncmdSoRCStLVq/iKaWpnZtTS1NLFq/KKCIYrf9mmvZfs21QYchIlkmloTM/J+XAEucc5vatEmKmXHfi8y478Wgw5Ast2v/rrjaRUSyXSwJ2TozewovIXvSzPoBh5MblkiGql0KO6ph+xpYMMp7nIEG9h0YV7uISLaLJSH7OjAXmOicOwD0QVMnicSvdilU3gwtn3iPG971HmdgUlY2oYzcnNx2bbk5uZRNKAsoIhGR1BbL1EmHzewt4HNmltvZ+iISwTPz4WBj+7aDjV77mCuCiSlJSoZ4ddbmrZ1H8+FmCvoWUDahrLVdRETa6zQhM7N/BMqAwcBG4BzgRQK80tLMSoHSoUOHBhWCSPwadsTXnuZKhpSw7LVlACy5aEnA0cSmobKSxk2bcM3NvD51GgNmzyK/tDTosEQkC8TSZVkGTAS2O+emAOOBPUmNqhPOuUrn3PX5+flBhiESn/zB8bWniGyZj7KhspL62+fhmr1SHYfq6qi/fR4NlZUBRyYi2SCWhKzJOdcEYGZHO+deBYYlNyzpihUbdrLhnb386a0PKb7zWVZs2Bl0SNLWtHnQO699W+88r10C996Chbim9qU6XFMT7y1YGExAIpJVYplcfIeZ9QdWAE+b2V+AumQGJfFbsWEntyx/ieYW7wLYnXsbuWX5SwBcOn5QkKFJSGic2G9v9Ab255/sJWMZNn4sXR2qr4+rXUSkO8UyqP8y/265ma0C8oEnkhqVxO2uJ7fSeLClXVvjwRbuenKrErJUMuYKWPegd3+mqtankl4FBRyqO/J/zV4FBQFEIyLZJpYzZK2cc6uTFYgkpm5vY1ztIj0hXQbzAwyYPcsbQ9am29Jycxkwe1ZwQYlI1ohlDJmkgcL+eXG1i2Syrkx/lF9aSsEd87E+fQDoVVhIwR3zdZWliPQIJWQZYs6Fw8jrndOuLa93DnMu1PUX0nVV26qo3VNLze4api+bnvGTg+eXlpI3dizHTJzImc8+o2RMRHpMTAmZmZ1qZn/l38/zp0+SFHLp+EH8+Cuj6ZPjvaWD+ufx46+M1vgx6bKqbVWUv1BO82GvDET9/nrKXyjP+KRMRCQInSZkZvYNYBlwn980GO+KS0kxl44fxPhT+vP5049n7dypSsYkIYvWL6KppX0ZiKaWJhatXxRQRCIimSuWQf3/D5gE/AnAOfe6mQ1IalQimSxNrq7ctX9XXO0iItJ1sXRZfuKcaw49MLNegEteSCKSCgb2HRhXe6oITX90oLqa16dOU6V9EUkLsSRkq83sX4A8M/sS8CigbzhJf0tKvFtPb5smyiaUkZuT264tNyeXsgllAUXUOU1/JCLpKpYuy7nA14GXgG8CK4EHkhmUiASvZIiXcM5bO4/mw80U9C2gbEJZa3sqijb9UaxXTJ768EPJCE1EJKpYKvUfBn7u30Qki5QMKWHZa8uA9CjyqumPRCRddZqQmdlLHDlmrAGoAf7VOfdBMgITke4z84mZQHokVSGhwq7xnLHS9Ecikq5iGUP2OFAFXO3fKoHngV3Ar5IWmYhInAbMnoXlth/3pumPRCQdxDKGrNg5V9zm8UtmttY5V2xm/5CswKRrKr55btAhiAQmNE6s/tbbcM3N9CosZMDsWaq4LyIpL5aE7Fgz+7xz7k8AZjYJONZfdihpkYmIdEF+aSl7lz4KaIC+iKSPWLos/xF4wMzeMrO38a6w/IaZ9QV+nMzgRJKmdinsqIbta2DBKO9xT2wrIiISRixXWVYDo80sHzDn3N42i/WXSNJP7VKovBlaPvEeN7zrPQYYc0XythUREYkgli5LzKwEGAnkmhkAzrn5SYxLJHmemQ8HG9u3HWz02jtLqhLZNk2l05WZIiLpKpbJxf8LmAHcBBjwd8CpSY5LJHkadsTX3l3bBqRqWxW1e2qp2V3D9GXTqdqW+nNpavojEck2sYwhO885dy3wF+fcD4BzgZOTG5ZIEuUPjq+9u7YNQNW2KspfKKf5sDeVUP3+espfKE/ppEzTH4lINoolIQvNQ3LAzAqBg8DpyQtJJMmmzYPeee3beud57cncthvMfGJma5HXWCxav4imlvZTCTW1NLFo/aLuDi2s7ddc21rgNVbRpj8SEclUsYwhqzSz/sBdwHq8qv2aRknSV2is129v9Abn55/sJVSxjAFLZNsA7Nq/K672VNAd0x+p3IWIpJuoCZmZHQU8419Z+Rsz+z2Q65xr6IngRJJmzBWw7kHv/sw4u+8S2baHDew7kPr9RyYyA/sODCCa2Gj6IxHJRlG7LP2Jxf+9zeNPlIyJpI+yCWXk5rSfSig3J5eyCWUBRdQ5TX8kItkoljFkT5nZ31qo3oWIpI2SISWUn1dOn6P6AFDQt4Dy88opGVIScGSR5ZeWUnDHfKyPF3OvwkIK7piv6Y9EJKPFMobs20BfoMXMGvFKXzjn3HFJjUxEukXJkBKWvbYMSJ+aYpr+SESyTSyV+vv1RCBmdj5wNV5MI5xz5/XE84qIiIgELZbCsGZm/2Bmt/uPT/YnGO+Umf3SzN4zs5c7tF9kZlvN7A0zmwvgnPs/59wNwO+BB+N/KZKVlpR4N0marpSuEBGR+MQyhuw/8IrB/r3/+GPg3hj3/yvgorYNZpbjb38xMAK4ysxGtFnl74FHYty/SNZIt4r7qrYvIhK7WBKyzzvn/h9+gVjn3F+APrHs3Dn3PPBhh+ZJwBvOuW3OuWbgf4EvA5jZKUCDc25fjPGLZIV0q7ivavsiIvGJJSE76J/VcgBm9lngcALPOQh4t83jHX4bwNeBqKOOzex6M6sxs5o9e/YkEIZI+gi64n68VG1fRCQ+sVxluRh4DBhgZj8ELgduS+A5w5XPcADOue93trFz7n7gfoCioiKXQByS7RIp6trDBWHTreJ+d1TbFxHJJrFcZfk/ZrYOmIaXTF3qnHslgefcQfvJyQcDR5blFpFW6VZxX9X2RUTiE8tVlouA451z9zrn7kkwGQOoBs40s9PNrA9wJfC7BPcpktHSreK+qu2LiMQnli7L9cBtZvY5vK7LCudcTSw7N7NHgAuAE81sB/B959wvzOxG4EkgB/ilc25zl6IXyRKhyvrz1s6j+XAzBX0LKJtQlrIV90NV9etvvQ3X3EyvwkIGzJ4VV7V9FYQVkWwSS5flg8CDZnY88LfAv5nZKc65M2PY9qoI7SuBlfEGG2JmpUDp0KFDu7qLlDbjvhcBqPjmuQFHIskw84mZQPxV8xOpuB9EhX5V2xcRiV0sV1mGDAWGA6cBryYlmhg55yqdc9fn5+cHGYYErXYp7KiG7WtgwSjvsXQr1RITEekZsYwh+zczex2YD2wGznbOaZZfCVbtUqi8GVo+8R43vOs9VlLWbVRLTESk58Ryhuwt4Fzn3EXOuV865/YmOSaRzj0zHw42tm872Oi1S7dQLTERkZ4Tyxiy/zKzz/jzV+a2aX8+qZGJRNOwI752iZtqiYmI9JxYuiz/EXge76rIH/g/y5MbVqcxlZrZ/Q0NDUGGIUHKHxxfu8QtUs0w1RITEel+sXRZlgETge3OuSnAeCDQOYs0qF+YNg9657Vv653ntUu3UC0xEZGeE0sdsibnXJOZYWZHO+deNbNhSY9MJJoxV3g/f3ujN7A//2QvGQu1Szvbr7kWiK/8RHfUEhMRkdjEkpDtMLP+wArgaTP7C5rqSFLBmCtg3YPe/R6eWzJbqJaYiEjPiGVQ/2X+3XIzWwXkA08kNSoRERGRLBLLGbJWzrnVyQpEREREJFvFlZBJ8q3YsJMN7+ylueUwxXc+y5wLh3Hp+EFBhyXdpGpbFbV7amk+3Mz0ZdPjno8yiCmQEqFuThGR2MQzdVLKyNSyFys27OSW5S/R3HIYgJ17G7ll+Uus2LAz4MikO1Rtq6L8hXKaD3uV7+v311P+QjlV2zT+TUQk26VlQpapZS/uenIrjQdb2rU1Hmzhrie3BhSRdKdF6xfR1NK+8n1TSxOL1i8KKCIREUkVaZmQZaq6vY1xtUt62bV/V1ztIiKSPZSQpZDC/nlxtUt6Gdh3YFztIiKSPZSQpZA5Fw4jr3dOu7a83jnMuVB1eDNB2YQycnPaV77PzcmlbEJZQBGJiEiqUEKWQi4dP4gff2U0fXK8t2VQ/zx+/JXRusoyQ5QMKaH8vHL6HNUHgIK+BZSfVx7XVZZd0VBZSeOmTRyorub1qdNoqKxM6vOJiEj8VPYixVw6fhCP/PkdACq+eW7A0UgkM5+YCcRfhqJkSAnLXlvWpW27oqGykvrb5+GavSs7D9XVUX+7N9+npkASEUkdaXmGLFPLXmStJSXeTbrdewsW4praX9npmpp4b8HCYAISEZGw0vIMmXOuEqgsKir6RtCxSMA0h2VUh+rr42oPR8VdRUSSLy3PkIlIbHoVFMTVLiIiwVBCJpLBBsyeheW2v7LTcnMZMHtWMAGJiEhYadllKSKxCQ3cr7/1NlxzM70KCxkwe5YG9IuIpBglZCIZLr+0lL1LHwU0HkxEJFWpyzJJZtz3IjPuezHoMERERCQNKCGTrDXziZmt9cRERESCpIRMREREJGBpmZCpMKyIiIhkkrRMyJxzlc656/Pz84MORURERCRhaZmQiYiIiGQSJWQSrNqlsKMatq+BBaO8xymualsVtXtqqdldw/Rl06napumbREQkMUrIJDi1S6HyZmj5xHvc8K73OIWTsqptVZS/UE7z4WYA6vfXU/5CuZIyERFJiArDpqCKb54bdAg945n5cLCxfdvBRq99zBXBxNSJResX0dTS1K6tqaWJResXUTKkJKZ9LLloSTJCExGRNKYzZBKchh3xtaeAXft3xdUuIiISCyVkEpz8wfG1p4CBfQfG1S4iIhILJWQSnGnzoHde+7beeV57iiqbUEZuTm67ttycXMomlAUUkYiIZAKNIZPghMaJ/fZGb2B//sleMpai48eA1nFi89bOo/lwMwV9CyibUBbz+DEREZFwlJBJsMZcAese9O7PTI8rFUuGlLDstWVA+gzQP/Xhh4IOQUREokjLLktNnSQiIiKZJC0TslSfOmnFhp1seGcvf3rrQ4rvfJYVG3YGHZJ0oOKuIiKSStIyIUtlKzbs5JblL9HcchiAnXsbuWX5S0rKUoiKu4qISKpRQtbN7npyK40HW9q1NR5s4a4ntwYUkXQUrbiriIhIEJSQdbO6vY1xtUvPU3FXERFJNUrIullh/7y42qXnqbiriIikGiVk3WzOhcPI653Tri2vdw5zLhwWUETSkYq7iohIqlEdsm526fhBAHx3WS3NLYcZ1D+PORcOa22X4Km4q4iIpBolZElw6fhBPPLndwCo+Oa5AUfTQ5b4yYyKuybV9muuBVToVUQk06jLUkRERCRgSshEREREAqaETERERCRgSshEREREAqaETERERCRgaZmQmVmpmd3f0NAQdCgiIiIiCUvLhMw5V+mcuz4/Pz/oUEREREQSlpYJmYiIiEgmUWFYCV6aFJMVERFJFp0hExEREQmYzpCJdEE6TbckIiKpT2fIRERERAKmhExEREQkYErIRERERAKmhExEREQkYErIRHrY9muuZfs11wYdhoiIpBAlZCIiIiIBU0ImiatdCjuqYfsaWDDKeyzdrqGyksZNmzhQXc3rU6fRUFkZdEgiItJNlJBJYmqXQuXN0PKJ97jhXe+xkrJu1VBZSf3t83DNzQAcqquj/vZ5SspERDKEEjJJzDPz4WBj+7aDjV67dJv3FizENTW1a3NNTby3YGEwAYmISLdSpX5JTMOO+NpTSDpV2z9UXx9Xu4iIpBedIZPE5A+Or126pFdBQVztIiKSXpSQSWKmzYPeee3beud57dJtBsyeheXmtmuz3FwGzJ4VTEAiItKt1GWZJBXfPDfoEHrGmCu8n7+90RvYn3+yl4yF2qVb5JeWAlB/62245mZ6FRYyYPas1nYREUlvSsgkcWOugHUPevdnVgUbSwbLLy1l79JHATj14YcCjkZERLpTWnZZmlmpmd3f0NAQdCgiIiIiCUvLhMw5V+mcuz4/Pz/oUEREREQSlpYJmYiIiEgmUUImIiIiEjAlZCIiIiIBU0ImIiIiEjAlZCIiIiIBU0ImIiIiEjAlZCIiIiIBU0ImIiIiEjAlZCIiIiIBU0Im0oMaKitp3LSJA9XVvD51Gg2VlUGHJCIiKUAJmUgPaaispP72ebjmZgAO1dVRf/s8JWUiIqKETKSnvLdgIa6pqV2ba2rivQULgwlIRERShhIykR5yqL4+rnYREckeSshEekivgoK42kVEJHsoIRPpIQNmz8Jyc9u1WW4uA2bPCiYgERFJGb2CDkAkW+SXlgJQf+ttuOZmehUWMmD2rNZ2ERHJXkrI5FNLSryfM6uCjSMOM5+YCcCSi5bEve32a64F4NSHH+qxbfNLS9m79NEuP6+IiGQmdVmKiIiIBEwJmYiIiEjAlJCJiIiIBEwJmYiIiEjAlJCJiIiIBEwJmYiIiEjAlJCJiIiIBEwJmYiIiEjAlJCJiIiIBEwJmYiIiEjAlJCJiIiIBCxl5rI0s6OAO4DjgBrn3IMBhyQiIiLSI5J6hszMfmlm75nZyx3aLzKzrWb2hpnN9Zu/DAwCDgI7khmXiIiISCpJ9hmyXwH3AA+FGswsB7gX+BJe4lVtZr8DhgEvOufuM7NlwDNJjk2608yqoCPICqc+/FDnK4mISNpJ6hky59zzwIcdmicBbzjntjnnmoH/xTs7tgP4i79OSzLjEhEREUklQQzqHwS82+bxDr9tOXChmf0MeD7SxmZ2vZnVmFnNnj17khupiIiISA8IYlC/hWlzzrkDwNc729g5dz9wP0BRUZHr5thEREREelwQZ8h2ACe3eTwYqAsgDhEREZGUEERCVg2caWanm1kf4ErgdwHEISIiIpISkl324hHgRWCYme0ws6875w4BNwJPAq8AS51zm5MZh4iIiEgqS+oYMufcVRHaVwIru7pfMysFSocOHdrVXYiIiIikjLScOsk5V+mcuz4/Pz/oUEREREQSlpYJmYiIiEgmUUImIiIiEjAlZCIiIiIBS8uEzMxKzez+hoaGoEMRERERSVhaJmQa1J8EtUthRzVsXwMLRnmPU1zVtipq99RSs7uG6cumU7Ut9gnOGyorady0iQPV1bw+dRoNlZU9sq2IiEg4aZmQSTerXQqVN0PLJ97jhne9xymclFVtq6L8hXKaDzcDUL+/nvIXymNKyhoqK6m/fR6u2dv2UF0d9bfPiymxSmRbERGRSJSQCTwzHw42tm872Oi1p6hF6xfR1NLUrq2ppYlF6xd1uu17Cxbimtpv65qaeG/BwqRuKyIiEokSMoGGHfG1p4Bd+3fF1d7Wofr6uNq7a1sREZFIlJAJ5A+Orz0FDOw7MK72tnoVFMTV3l3bioiIRKKETGDaPOid176td57XnqLKJpSRm5Pbri03J5eyCWWdbjtg9iwst/22lpvLgNmzkrqtiIhIJEmdyzJZNJdlNxtzhffztzd6A/vzT/aSsVB7CioZUgLAvLXzaD7cTEHfAsomlLW2R5NfWgpA/a234Zqb6VVYyIDZs1rbk7WtiIhIJOacCzqGLisqKnI1NTVBh5E5lvjJzMzYy0cEbeYTMwFYctGSuLfdfs21AJz68ENps62IiKQvM1vnnCsKt0xdliIiIiIBU0ImIiIiEjAlZCIiIiIBU0ImIiIiEjAlZCIiIiIBS8uEzMxKzez+hoaGoEMRERERSVhaJmTOuUrn3PX5+flBhyIiIiKSsLRMyEREREQyiRIyERERkYApIRMREREJmBIyERERkYApIRMREREJmBIyERERkYApIRMREREJWK+gA+gKMysFSocOHRp0KCJxO/Xhh4IOQUREUow554KOocvMbA+wPYZVTwTeT3I4mULHKnY6VrHRcYqdjlVsdJxip2MVu544Vqc65z4bbkFaJ2SxMrMa51xR0HGkAx2r2OlYxUbHKXY6VrHRcYqdjlXsgj5WGkMmIiIiEjAlZCIiIiIBy5aE7P6gA0gjOlax07GKjY5T7HSsYqPjFDsdq9gFeqyyYgyZiIiISCrLljNkIiIiIikrYxIyMzvZzFaZ2StmttnMysKsc4GZNZjZRv82L4hYU4GZvW1mL/nHoSbMcjOzxWb2hpnVmtmEIOIMkpkNa/NZ2Whm+8xsVod1svYzZWa/NLP3zOzlNm3Hm9nTZva6//MzEba9yMy2+p+vuT0XdTAiHKu7zOxV//frMTPrH2HbqL+rmSTCcSo3s51tfscuibCtPlNmFW2O09tmtjHCttn0mQqbG6Tkd5VzLiNuQAEwwb/fD3gNGNFhnQuA3wcdayrcgLeBE6MsvwR4HDDgHOBPQccc8PHKAXbh1ZBp2561nylgMjABeLlN20+Auf79ucC/RTiWbwJDgD7Apo6/q5l2i3CspgO9/Pv/Fu5Y+cui/q5m0i3CcSoH/rmT7fSZOnL5vwPzIizLps9U2NwgFb+rMuYMmXOu3jm33r//EfAKMCjYqNLal4GHnOePQH8zKwg6qABNA950zsVSiDgrOOeeBz7s0Pxl4EH//oPApWE2nQS84Zzb5pxrBv7X3y5jhTtWzrmnnHOH/Id/BAb3eGApJsJnKhb6TLVhZgZcATzSo0GloCi5Qcp9V2VMQtaWmZ0GjAf+FGbxuWa2ycweN7ORPRtZSnHAU2a2zsyuD7N8EPBum8c7yO4E90oif7npM/Wpk5xz9eB9EQIDwqyjz9aRrsM7Ix1OZ7+r2eBGv2v3lxG6lvSZau98YLdz7vUIy7PyM9UhN0i576qMS8jM7FjgN8As59y+DovX43U5jQV+Bqzo4fBSSbFzbgJwMfD/zGxyh+UWZpusvCTXzPoAfwM8GmaxPlPx02erDTO7FTgE/E+EVTr7Xc10/wmcAYwD6vG64jrSZ6q9q4h+dizrPlOd5AYRNwvTlrTPVUYlZGbWG++A/49zbnnH5c65fc65j/37K4HeZnZiD4eZEpxzdf7P94DH8E7NtrUDOLnN48FAXc9El3IuBtY753Z3XKDP1BF2h7q2/Z/vhVlHny2fmX0V+GvgaucPWukoht/VjOac2+2ca3HOHQZ+TvjXr8+Uz8x6AV8BKiKtk22fqQi5Qcp9V2VMQub3mf8CeMU5d3eEdQb662Fmk/Be/wc9F2VqMLO+ZtYvdB9vcPHLHVb7HXCtec4BGkKnd7NQxP829Zk6wu+Ar/r3vwr8Nsw61cCZZna6f/bxSn+7rGJmFwHfA/7GOXcgwjqx/K5mtA5jVy8j/OvXZ+pTfwW86pzbEW5htn2mouQGqfddFfQVEN11A76AdyqxFtjo3y4BbgBu8Ne5EdiMd6XEH4Hzgo47oGM1xD8Gm/zjcavf3vZYGXAv3hUmLwFFQccd0LE6Bi/Bym/Tps+U99ofwetCOoj3n+TXgROAZ4DX/Z/H++sWAivbbHsJ3tVOb4Y+f5l8i3Cs3sAbnxL6vvqvjscq0u9qpt4iHKeH/e+gWrw/hgX6TIU/Vn77r0LfT23WzebPVKTcIOW+q1SpX0RERCRgGdNlKSIiIpKulJCJiIiIBEwJmYiIiEjAlJCJiIiIBEwJmYiIiEjAlJCJiIiIBEwJmYikDTMrN7N/9u/PN7O/irLupWY2oueiC/v88zq0bTKzRzq0/dTMpvZsdCKSapSQiUhacs7Nc879IcoqlwKBJWTAd4H/CD0ws7PwvnMn+xXSQ34GzO3h2EQkxSghE5GUZma3mtlWM/sDMKxN+6/M7HL//p1mtsXMav0zTufhTQh/l5ltNLMzzOwbZlbtn6X6jZkd02Y/i83sBTPbFtqnv+y7ZvaSv82dftsZZvaEma0zs/8zs+FhYv4c8Ilz7v02zX+PV3X+KT82AJxz24ETzGxgNx42EUkzvYIOQEQkEjM7G2/+uPF431frgXUd1jkeb47D4c45Z2b9nXN7zex3wO+dc8v89fY6537u3/9XvGl5fubvpgBvipXheNPzLDOzi/HOsn3eOXfAfx6A+/GmpnndzD6PdxasY5djsR9rWzOAL+EllTfSfn7U9f42v4nn+IhI5lBCJiKp7HzgMedPvu0nWR3tA5qAB8ysCvh9hH2N8hOx/sCxwJNtlq1wzh0GtpjZSX7bXwFLQs/tnPvQzI4FzgMe9eeUBzg6zHMVAHtCD8xsIrDHObfdzHYAvzSzzzjn/uKv8h7eHHoikqXUZSkiqS7qhLvOuUPAJLyzS5cCT0RY9VfAjc650cAPgNw2yz5pc9/a/Oz43EcBe51z49rczgrzXI0d9n8VMNzM3sabpPg44G/bLM/1txGRLKWETERS2fPAZWaWZ2b9gNKOK/hnrfKdcyuBWcA4f9FHQL82q/YD6s2sN3B1DM/9FHBdm7Fmxzvn9gFvmdnf+W1mZmPDbPsKMNRf5yjg74AxzrnTnHOnAV/GS9JCPge8HENMIpKhlJCJSMpyzq0HKoCNeGfA/i/Mav2A35tZLbAamO23/y8wx8w2mNkZwO3An4CngVdjeO4n8MaT1ZjZRuCf/UVXA183s03AZrzkqqPngfHm9WtOBnY653Z2WD7CzAr8BHEoUNNZTCKSucy5qL0BIiLSBWa2CKjspDQHZnYZMME5d3vPRCYiqUhnyEREkuNHwDExrNcL+PckxyIiKU5nyEREREQCpjNkIiIiIgFTQiYiIiISMCVkIiIiIgFTQiYiIiISMCVkIiIiIgH7/zuK8aVO27z9AAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_errorbar_kinetics(kin, useCaseDir, 'SDA_bootstrap_ratecurve.png')"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Ld4GbynFuwR2"
},
"source": [
"In the figure above, the average association rate constant is plotted on a logarithmic scale against the contact distance in Å when 1 to 4 contacts between the two solutes, as defined by the reaction criteria, are shorter than the contact distance. One can see that the association rate constant decreases the closer the solutes come to each other. It also decreases as the number of contacts that have to be satisfied increases. These trends can be explained by the decreasing number of ways the two solutes can arrange with respect to each other as the reaction criteria become more stringent. From this plot, the association rate constant for a given reaction criterion can be extracted and used for further modeling. \n",
"\n",
"In this example, we estimate the the rate constant of Gαolf associating to AC5 using a reaction criterion of two contacts at a distance of 6 Å.\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "sNIzhpWxuwR2",
"outputId": "ca4ba5bf-a5df-49f0-8a5d-9fa0693eacad"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Association rate constant = 4.46e+06 +/- 1.63e+06 M-1s-1\n"
]
}
],
"source": [
"# Read association rate from data frame\n",
"row = kin[1].loc[kin[1]['distance'] == '6.000']\n",
"rate = row['average'].values[0]\n",
"stddev = row['std.deviation'].values[0]\n",
"\n",
"print('Association rate constant = %9.2e +/-%9.2e M-1s-1' % (float(rate), float(stddev)))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "U5oADsTgRkEV"
},
"outputs": [],
"source": []
}
],
"metadata": {
"colab": {
"provenance": []
},
"kernelspec": {
"display_name": "EBRAINS-23.02",
"language": "python",
"name": "ebrains-23.02"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.11"
}
},
"nbformat": 4,
"nbformat_minor": 4
}