effective (potential derived) charges for macromolecules in solvent
version 2.00
EMBL, Heidelberg
Mon Jan 19 11:11:11 MET 1998
Revised version integrated into SDA 7, October 2013, MM.
R.R. Gabdoulline & R.C. Wade. Effective
charges for macromolecules in solvent
J.Phys.Chem. (1996) 100, 3868-3878
In order to study protein-protein and protein-DNA association, the electrostatic forces and interaction free energies for two macromolecules at different mutual orientations and separations need to be evaluated. Realistic systems typically consist of thousands of atomic charges in an environment with a non-uniform dielectric permittivity and a solvent of non-zero ionic strength. Consequently, accurate evaluations of electrostatic forces and energies for such systems are only computationally feasible for a limited number of macromolecule positions. Here, we show that, by representing each molecule by a small number of effective charges in a uniform dielectric, intermolecular electrostatic interactions can be calculated simply and with high accuracy. The effective charges are derived by fitting them to reproduce the molecular electrostatic potential calculated by numerical solution of the finite-difference linearized Poisson-Boltzmann equation. The derived charges are expected to be useful in applications such as the simulation of the diffusional encounter of proteins where they will provide improved accuracy over the commonly-used test charge approximation.
- These are fitted charges that, when immersed in a uniform dielectric, give the electrostatic potential of the molecule computed in a heterogeneous dielectric. They can reproduce the electrostatic potential of a protein computed with the use of all atomic charges with an accuracy of 5-10%, however assigning effective charges only to 1 or 2 atoms of the side-chains of the titratable residues.
- The fitting is similar to that used in the CHELP procedure to obtain atomic charges for small molecules: it is done over a layer of reasonable thickness around the molecule (a molecular skin).
- As in the finite difference calculations, the effective charges can be used to compute interaction energies and forces between two macromolecules taking into account the complex molecular shapes, a low dielectric cavities inside the molecules and the ionic strength of the solvent surrounding the molecules. The advantage of the effective charges is that the computations are much faster than solving e.g., PB equation for each two solute configuration. Moreover, these effective charges take into account any mutual influence of the charges of atoms surrounding, therefore, the cost of calculations is only linearily increasing with the number of effective charges.
- These effective charges not only offer a fast evaluation of the energy, but they are also free of the grid spacing problems that are encountered in finite difference methods: the fitting results are not sensitive to the grid spacing used to compute potentials, within the error estimate mentioned above.
- Model cases:
- a dipole (2 charges of opposite sign at close separation) at the center of low dielectric sphere surrounded by high dielectric continuum gets rescaled by a factor of 1.5;
- a charge at the center of non-ionic sphere of radius a surrounded by ionic solvent with Debye-Hückel parameter k gets rescaled by a factor of exp(ka)/(1+ka).
BEFORE using the programs the user should have 2 files and know 2 parameters:
- pdb_file - the coordinates of the macromolecule used to compute the electrostatic potential in Brookhaven protein databank format;
- grd_file - electrostatic potential grid in UHBD format computed for the macromolecule in exactly the same orientation and position;
- ionic strength of the solvent - it should be identical to the value used for generating the electrostatic potential
- dielectric permittivity of the solvent - the default value is 78., but can be adjusted
Version 2.00 notes.
Version 2 allows the charges to be fitted for an angular region of
the potential. The user needs to specify coordinates
of 2 points
(x1dir(3) and x2dir(3)) and the restriction angle
(angleg, in grad)
in the file "angular.restriction". Then
any points forming an angle larger than angleg to the vector
(x2dir-x1dir) are omitted from the fitting procedure. Note, that the
order of the 2 points in this input file makes a difference. If there
are no data in the file "angular.restriction", the fitting
procedure does not perform angular restriction.
There are 4 programs for effective charges generation:
I.ecm_mksites
usage: ecm_mksites file.pdb [file.tcha]
reads in pdb file,
locates the sites for effective charges,
assigns them the test charge value and writes to the output file in a PDB format with charges given in the last column.
The output file is optional.
comment: Only test charges for OE* OD* NZ NE* atoms of Glu, Asp, Lys, Arg, and N & O* of NTR and CTR terminal residues are coded in the current program. The user may use the add_atoms to overwritte or provide new definitions.
II.ecm_expand
usage: ecm_expand ecm.in
Expands the electrostatic potential of a macromolecule as given by a set of effective charges in uniform solvent. The resultant effective charges are given in the last column of a PDB format file output in "echa_file". In addition, the matrix for Coulomb-Coulomb, Coulomb-grid, grid-grid overlaps is written in file "matrix". (This is the most expensive part to compute.) The file "matrix" will be used by the subsequent regularization programs under this name. Standard output contains information about the performance of ecm_expand. This includes a simple graphics display of a cross-section of the region over which the potential fitting is performed. The user should check that this bears some resemblance to the shape of the protein under study.
It prints out the properties of the matrix equation for expansion. Namely, it exhaustively probes regularization of the matrix equation in the fitting problem equating the last N principal components of charges to the values derived from test charges. The output gives the N-dependence of the deviations (RMSD, see the definitions below) of the effective charge values from those of the test charges, the fitting error, the maximum deviation of any one effective charge from the respective test charge value (RM1D), the square root of the fitting error, and the sum of all the effective charges.
Comments
- The input script contains the names for: the pdb file, the grid file, the charge sites file generated by ecm_mksites, the name for a file to write effective charges in.
- The program uses LINPACK routine dgesl() to solve the linear system of equations.
- The program uses EISPACK routine rs() to perform matrix diagonalization.
Definitions
- RMSD =
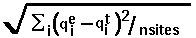 , where
, where 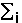 means summation over i=1,...,nsites,
means summation over i=1,...,nsites, 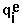 - effective charge on site i,
- effective charge on site i,
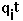 - test charge on site i.
- test charge on site i.
- RM1D =
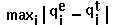 .
.
- fitting_error =
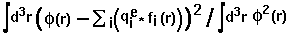 ,
where
,
where 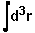 means integration over fitting region,
means integration over fitting region, 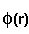 - electrostatic
potential of a macromolecule,
- electrostatic
potential of a macromolecule, 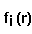 - Coulomb-Debye potential of a unit
charge in a uniform solvent. One should mentally take a square root from
this in order to imagine errors in the magnitude of the fitting potential,
even though the definition is standard.
- Coulomb-Debye potential of a unit
charge in a uniform solvent. One should mentally take a square root from
this in order to imagine errors in the magnitude of the fitting potential,
even though the definition is standard.
Advice: If the fitting results are satisfactory, don't go further. However, save the file "matrix" if you want to probe different regularizations later.
You can check the correctness of the assigned charges by loading the output file into a molecular visualization program and colouring the atom types by temperature factor, which reflects the effective charge in this file
III.ecm_mkreglev
usage: ecm_mkreglev [-reg_level 25] [-reg_charge 1.0]
(automatically reads from file "matrix")
To use for generating effective charges at a given iteration (reg_level) OR at a charge value (reg_charge), i.e., uses only one of these two options. You have to choose this level according to the iteration regularization generated by the previous program.
IV.ecm_all
usage: ecm_all -fp p1_noh.pdb -fg ep.grd -is 150. -rc 1.0 -fe p1_noh.echa
Execute all previous steps in one process. This tool accepts only arguments in command line (no input file is needed).
To generate effective charges with intermediate steps:
- ecm_mksites p1_noh.pdb
- ecm_expand ecm.in
- optional ecm_mkreglev -reg_level 35
In one step:
- ecm_all -fp p1_noh.pdb -fg ep1.bin.grd -is 150. -rc 1.0 -fe p1_noh.echa
- (optional) ecm_mkreglev -reg_level 35
A step-by-step procedure is described in the tutorial (section 4.) and examples of usage are given in preapre_grids_and_ecm/ subfolders of the examples.
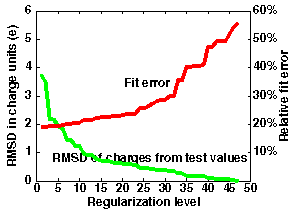
The left graph in the figure below shows the meaning of optimization when using regularized charges.
In this example, 47 charge sites were used to fit the potential over distances 5-8 Angstroms from the van der Waals surface of the macromolecule in file "1brsA.pdb".
-
The maximum accuracy is obtained without regularization (N=0) when the standard classical error is 0.037.
This corresponds to an average error of 19% in the computed potential values. - For test charges (N=47), the standard error is 0.31 corresponding to an error of 56% in the potential.
However, the most accurate effective charges deviate from "reasonable" test charge values (+-0.5,1.0) by 3.5 units on average. Examination of the error curve shows that if the regularization level is chosen at N=20, the error in the potential is only 23%, and the charges deviate from test charge values by an average of only 0.6 units (and have a maximal deviation (RM1D) of 1.9 - this is seen from the output of ecm_regularize). - Better accuracy of 20% is given by N=10, with an RMSD for effective charges of 1.2 and an RM1D of 3.2.
- Poorer accuracy of 29% is given by N=30, with an RMSD for effective charges of 0.4 on average and an RM1D of 0.8.
Automated optimization is difficult even in this case. The error increase with optimization level allows at least the 3 above mentioned optimum choices.
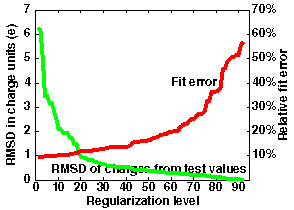
If one wants to use more sites, the curve would look different. An example is given in the right graph in the figure below, where 92 charge sites are used.
Here, regularization at level 40 allows approximation of the potential within an error of 14% and with RMSD deviation of charges 0.55 (RM1D - 1.6). The smallest fit error is 10%, compared to 20% in the previous case.